Cea mai mare valoare a expresiei
Pentru a găsi cea mai mare valoare de expresii trigonometrice, în multe cazuri, este suficient să se cunoască valoarea suprafață de sinus, cosinus, tangenta, cotangentă și proprietățile inegalităților.
Găsiți valoarea maximă a expresiei:
Intervalul valorilor admise ale acestei expresii - întreaga linie numărul:
Valorile cosinus FIELD - intervalul [-1; 1]. Pentru a evalua valoarea este mai convenabil de a utiliza dubla inegalitate:
Înmulțiți termen de termen privind inegalitatea 7. Când înmulțit cu numărul de semne pozitive de inegalitate nu se schimbă:
Apoi se adaugă termenul de termenul 5:
Astfel, cea mai mare valoare expresiei este egală cu 12 (cele mai mici - -2, valorile zonei - [-2: 12]).
Atunci când este multiplicată cu un număr negativ semne de inegalitate sunt inversate:
Rescrie în ordine crescătoare
Adăugați termenul de termenul 4
Cea mai mare valoare expresiei este egală cu 7 (cel mai puțin - 1, intervalul de valori - [1, 7]).
Cea mai mare valoare expresie este egală cu 10 (cel mai mic - 8, intervalul de valori - [8, 10]).
(Notă: Dacă pre-converti expresia .:
este posibil să se simplifice evaluarea, deoarece nu este necesar să se multiplice inegalitatea de un număr negativ), în acest caz.
Soluție: Fracțiunea are sens, dacă numitorul nu este zero, deci DHS: sinα ≠ 0. Preferat lucrul cu DHS pe cercul unitate: punctele α = 0 și α = P, în care dispare sinα. perforări:
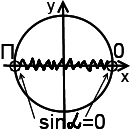
Rămâne să se estimeze expresia obținută.
Cu toate acestea, având în vedere DHS, avem:
(Cosα = 1 pentru α = 0, cosα = -1 când α = P).
Expresia nu acceptă maxim sau valori mai mici (aria de valori de expresie - (8; 10)).
Data viitoare va continua să ia în considerare expresiile cu fracții, și mai târziu - expresii de forma unui sinα + b ∙ cosα ∙.