Circumferinței și cerc

Raza cercului (cerc): \ (R \)
Diametrul cercului (cerc): \ (D \)
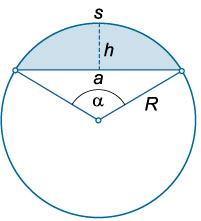
lungimea corzii: \ (a \)
segmente Chord: \ (\) \ (\) \ (\) \ (\)
Măsurile sau lungimea arcului: \ (s \) \ (\) \ (\)






Intersectând segmente: \ (e \) \ (\) \ (f \) \ (\)
Coordonatele centrului cercului: \ (\) \ (\)
Coordonatele cercului: \ (x \) \ (y \)
Înălțimea Segment: \ (h \)

Unghiul central: \ (\ alpha \), \ (x \)
Unghiul Inscripționată: \ (\ beta \)
Unghiul dintre acorduri: \ (\ varphi \)
Unghiul dintre intersectarea: \ (\ gamma \)
Unghiul dintre tangenta și secantă: \ (\ delta \)
Unghiul dintre tangenta și coarda: \ (\ theta \)
Unghiul dintre tangentele: \ (\ eta \)
Perimetru: \ (P \)
Zona: \ (S \)

Circumferința - este locul geometric al punctelor în plan echidistant față de un punct dat (centrul cercului). Distanța dintre orice punct de pe cercul și centrul său se numește raza cercului.

Segmentul care leagă două puncte ale cercului se numește o coardă. Coarda care trece prin centrul cercului este diametrul. Diametrul cercului este egală cu dublul razei:
\ (D = 2R \)

Unghiul central - unghiul vârful care coincide cu centrul cercului. Raportul dintre coardă și unghiul central este dată de:
\ (A = 2R \ păcatul \ mare \ frac \ normalsize \)

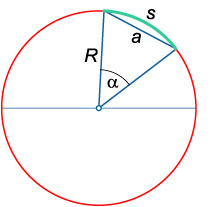
porțiune de arc numit conținea circumferențial între două puncte. Măsură arc (în grade sau radiani) este unghiul subîntins central de la acest arc. Lungimea arcului definit de relația
\ (S = \ alpha R \),
unde \ (\ alpha \) - un unghi central de exprimat în radiani, \ (R \) - raza cercului.

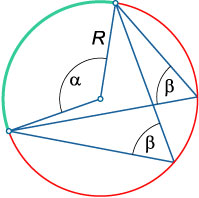
Unghiul Inscripționată - este un unghi al cărui vârf se află pe circumferința și unghiul Părțile să-l intersectează. Inscripționată unghi egal cu jumătate din centru, dacă cele două unghiuri se bazează pe același arc de cerc:
\ (\ Beta = \ mare \ frac \ normalsize \),

Punctul de intersecție a două acorduri la fiecare acord se împarte în segmente, al căror produs este aceeași:
\ (= \)

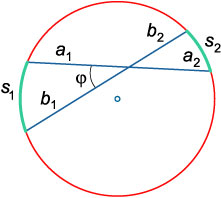
Unghiul dintre coardele care se intersectează este egală cu jumătate din suma arcurilor opuse tăiate acorduri:
\ (\ Varphi = \ mare \ frac + >> \ normalsize \),
în cazul în care \ (\) \ (\) - măsură cu arc (grade sau radiani).

Secțiunea transversală se numește linia dreaptă care trece prin două puncte distincte ale cercului. Pentru oricare două secants trase dintr-un punct arbitrar în afara cercului, produsul lungimii primei secțiunii transversale din partea sa exterioară este produsul din lungimea celei de a doua secțiune transversală din partea sa exterioară:
\ (E = f \)

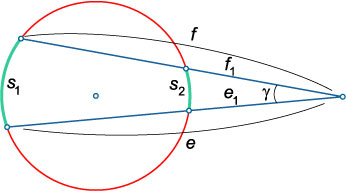
Unghiul dintre secantă. trase dintr-un punct arbitrar din afara circumferinței este pe jumătate arce de mai mari și mai mici taie secante date:
\ (\ Gamma = \ mare \ frac - >> \ normalsize \),
în cazul în care \ (\) \ (\) - măsoară arcele respective (grade sau radiani).

Pentru orice secțiune transversală și tangenta. trase dintr-un punct arbitrar în afara cercului, produsul lungimii de tăiere pe partea sa exterioară este egală cu pătratul lungimii tangentei:
\ (F = \)

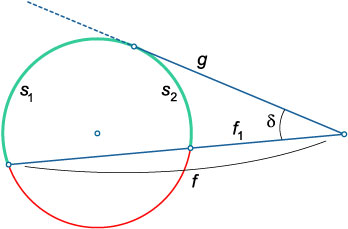
Unghiul dintre tangenta și secantă. trase dintr-un punct arbitrar, se taie jumătăți de arce:
\ (\ Delta = \ mare \ frac - >> \ normalsize \),
în cazul în care \ (\) \ (\) - măsoară arcele respective.

Unghiul dintre tangenta și coarda. care trece prin punctul de tangență, egală cu jumătate din arcul subîntins de o coardă:
\ (\ Theta = \ mare \ frac \ normalsize = \ mare \ frac \ normalsize \)

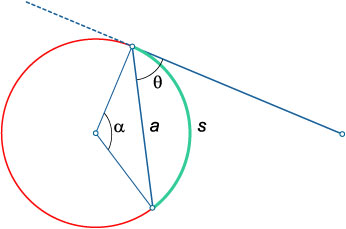
Tangent întotdeauna perpendicular pe raza efectuat la punctul de tangență.

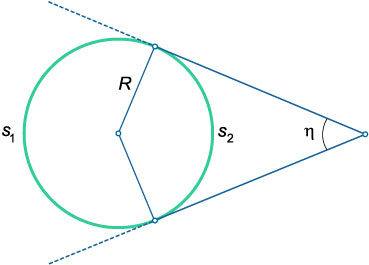
Unghiul dintre cele doua tangente. efectuate la circumferința punctului arbitrar, se taie o jumătate de arce:
\ (\ Eta = \ mare \ frac - >> \ normalsize \),
în cazul în care \ (\) \ (\) - măsoară arcele respective (grade sau radiani).

Ecuația cercului într-un sistem de coordonate cartezian
\ (> \ Dreapta) ^ 2> +> \ dreapta) ^ 2> = \)
în cazul în care \ (\) \ (\) - coordonatele centrului cercului, \ (R \) - raza, \ (\) - coordonatele punctelor circumferință.

Perimetrul unui cerc
\ (P = 2 \ pi R = \ pi D \)

Tot în jurul este partea a planului delimitat de un cerc și include centrul său.

Zona de cerc
\ (S = \ pi = \ mare \ frac >> \ normalsize = \ mare \ frac> \ normalsize \)

Gama de sector se numește o figură geometrică delimitată de două raze și un arc de cerc pe care datele sunt bazate pe raze.

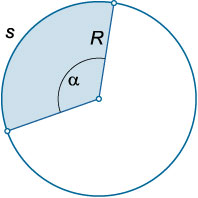
sectorul perimetru
\ (P = s + 2R \),
unde \ (s \) - lungimea arcului, \ (R \) - raza cercului.

Zona sectorului
\ (S = \ mare \ frac> \ normalsize = \ mare \ fracx >> \ normalsize = \ mare \ frac \ alfa >>> \ normalsize \),
unde \ (s \) - lungimea arcului, \ (R \) - raza cercului, \ (x \) - un unghi central în radiani, \ (\ alpha \) - un unghi central în grade.

Segment al unui cerc se numește o figură geometrică delimitată de o coardă și înăsprește arcului său.