Cum de a găsi piciorul de proiecție pe ipotenuza
Pentru a găsi media geometrică a unei serii de numere, trebuie mai întâi să multiplice toate aceste numere. De exemplu, vi se oferă un set de cinci indicatori: 12, 3, 6, 9 și 4. Noi multiplica toate aceste numere: 12h3h6h9h4 = 7776.
Acum, din numărul rezultat pentru a extrage o rădăcină de grad egal cu numărul de serie de elemente. În cazul nostru, numărul de 7776 va trebui să eliminați rădăcina gradul cinci, cu ajutorul calculatorului științific. Primite după această operație, numărul - în acest caz, numărul de 6 - va fi media geometrică pentru grupul inițial de numere.
Dacă nu aveți calculatorul meu științific, se calculează media geometrică a unei serii de numere, puteți utiliza funcția SRGEOM în Excel sau de a folosi una dintre calculatoare online proiectate special pentru a calcula media geometrică.
Dacă aveți nevoie pentru a găsi media geometrică a tuturor pentru două numere, calculatorul științific nu va fi nevoie: pentru a elimina rădăcina de gradul II (rădăcină pătrată) din orice număr este posibilă prin intermediul unui calculator obișnuit.
Spre deosebire de media aritmetică, geometrică nu înseamnă să afecteze atât de mult abateri mari și fluctuațiile între valorile individuale din setul de indicatori de testare.
- Calculator online care calculează media geometrică
- Formula medie geometrică
Într-un triunghi dreptunghic, există două tipuri de partide - latura scurtă a „picior“ și latura lungă a „ipotenuzei“. Dacă vom face o proiecție a piciorului la ipotenuzei, care este împărțit în două secțiuni. Pentru a determina valoarea uneia dintre ele, trebuie să vă înregistrați un set de date de intrare.

Datele inițiale ale problemei pot fi subscrise de lungime ipotenuzei D și lungimea piciorului N, a cărei proiecție pentru a găsi. Pentru a determina amploarea proiecției Nd, utilizați proprietățile unui triunghi dreptunghiular. Se determină lungimea piciorului A, folosind faptul că media geometrică, luată pe lungimea ipotenuzei și piciorul de proiecție, piciorul este egală cu valoarea dorită. Aceasta este, N = √ (D * Nd).
Având în vedere că rădăcină al produsului este aceeași ca și media geometrică pătratul valorii N (lungimea piciorului titlului), și se împarte la lungimea ipotenuzei. Aceasta este Nd = (N / √D) ² = N² / D.V lungimea datelor de intrare sunt valori pot fi date numai picioarelor N și T. în acest caz, lungimea proiecției Nd este găsit folosind teorema lui Pitagora.
Se determină lungimea ipotenuzei D, folosind valorile picioarelor √ (N² + T²) și înlocui valoarea rezultată într-o formulă pentru a găsi proiecții. Ce Nd = N² / √ (N² + T²).
Dacă datele sursă conține informații despre lungimea și mărimea proiecției Rd piciorul ipotenuzei D, lungimea proiecției celui de al doilea picior Nd calculat folosind o simpla scădere cu formula - Nd = D - Rd.
Într-o situație în care numai valoarea cunoscută a lungimii D a ipotenuzei, și având în vedere simplu raportul dintre lungimile picioarelor (m / h) o formulă de contact din prima etapă și a treia etapă.
Conform formulei primului pas, acceptă ca un fapt că raportul dintre proiecțiile Nd și Rd egal cu raportul dintre valorile pătrate de lungimea lor. Ie Nd / Rd = m / h². De asemenea, suma proiecțiilor picioarelor și Nd Rd egal cu lungimea ipotenuzei.
Exprimă valoarea proiecției prin cateta piciorului Rd dorit pentru a substitui Nd și o formulă însumare. Rezultatul este un Nd + Nd * m / h² = Nd * (1 + m / h²) = D, atunci puterea de a găsi formula Nd = D / (1 + m / h²). Valoarea Nd și va indica magnitudinea piciorului dorit.
Se numește triunghi dreptunghiular, dacă unghiul de unul dintre vertexului este de 90 °. Partea care se află vizavi de Vertex se numește ipotenuza, iar celelalte două - picioarele. Lungimile laturilor și unghiurile în această figură sunt interconectate prin aceleași rapoarte ca și în orice alt triunghi, dar din moment ce sinusul și cosinusul unghiului drept egal cu unu și zero, formula este simplificată în mod semnificativ.
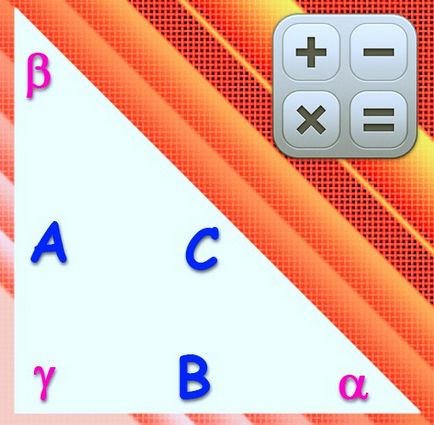
Dacă lungimea unuia dintre picioarele (a) și ipotenuzei (c) un triunghi dreptunghic sunt cunoscute, utilizate pentru a calcula lungimea celei de a treia parte (b) teorema lui Pitagora. Din aceasta rezultă că valoarea țintă trebuie să fie egală cu rădăcina pătrată a diferenței pătratului dintre lungimea și pătratul ipotenuzei picior lungime sub forma: b = √ (c²-a²).
Cunoscând unghiul (α) la vârful triunghiului de picior situată vizavi de lungime cunoscută (a), se poate calcula, de asemenea, lungimea necunoscută a doua etapă (b). Pentru a face acest lucru, se aplică definiția uneia dintre funcțiile trigonometrice - tangentă - pentru un unghi ascuțit. Din aceasta rezultă că lungimea piciorului necesar trebuie să fie egală cu mărimea unui anumit aspect, împărțit la tangenta unghiului opus: b = a / tg (α).
cotangentă Determinarea unghiului ascuțit de utilizat pentru a găsi lungimea piciorului (b) în cazul prezentat în ceea ce privește valoarea unghiului (β), adiacent la lungimea cunoscută alt catete (a). Formula general ar arata mult la fel ca în etapa anterioară, înlocuiți-l funcționa doar numele și desemnarea unghiului: b = a / ctg (β).
La o anumită lungime de ipotenuză (c) în calculul catete (b) determinarea dimensiunilor pot folosi trigonometrice de bază - sinus și cosinus - pentru unghiuri acute. În cazul în care, în condițiile date valoarea unghiului (α), între cele două părți ale celor două funcții trebuie să fie selectate cosinus. Multiplice lungimea ipotenuzei formei unghiului cosinus: b = c * cos (alfa).
sinus Determinarea utilizării în unghiurile acute unde lungimea ipotenuzei cu excepția (c) sunt date valoarea unghiului (β), la partea superioară, situată vizavi de cateta dorit (b). Formula de calcul, în general, este similar cu cel anterior - ar trebui să conțină produsul lungime ipotenuzei și sinusul dat valoarea unghiului: b = c * sin (β).