Cum de a găsi punctul de intersecție a graficelor

Orice program puteți seta o funcție specifică. Pentru a găsi acele puncte în care graficele se intersectează, este necesar să se rezolve o ecuație care are forma: f₁ (x) = f₂ (x). Rezultatul deciziei și voința punctului (sau puncte) pe care îl căutați. Luați în considerare următorul exemplu. Lăsați valoarea y₁ = k₁x + b₁, iar valoarea y₂ = k₂x + b₂. Pentru a găsi punctele de intersecție axa x necesare pentru a rezolva ecuația y₁ = y₂, adică k₁x + b₁ = k₂x + b₂.

Conversia această inegalitate a primit k₁x-k₂x = b₂-b₁. Acum exprimă x: x = (b₂-b₁) / (k₁-k₂). Astfel veți găsi intersecția topuri, care este situat la axa OX. Găsiți punctul intersectându pe axa y. Trebuie doar să înlocuiți în oricare dintre funcțiile de valoarea lui x, pe care ați găsit mai devreme.

Versiunea anterioară este potrivit pentru un grafic liniar al funcției. Dacă funcția pătratică, utilizați următoarele instrucțiuni. În același mod ca o funcție liniară, pentru a primi valoarea de x. Pentru a face acest lucru, pentru a alege o ecuație pătratică. În ecuația 2x² + 2x - 4 = 0 discriminant get (ecuația dată ca exemplu). Pentru aceasta se folosește formula: D = b² - 4ac, unde b - valoare înaintea X, și c - un număr de valoare.

Substituind valori numerice, obținem expresii de forma D = 4 * 4 + 4 = 4 + 16 = 20. Din valoarea discriminante depinde rădăcinile. Acum, valoarea variabilei b cu semnul „-“ adăuga sau scădea (succesiv) rădăcina discriminante obținut, și se împarte la de două ori produsul coeficientului a. Deci, veți găsi rădăcinile ecuației, adică coordonatele punctelor de intersecție.

grafice de funcții pătratice au o caracteristică: axa OX se va intersecta de două ori, adică, veți găsi două coordonate ale axa x. Dacă obțineți valoarea unei dependență periodică a X pe Y, atunci știu că graficul se intersectează cu un număr infinit de puncte cu axa x. Verificați dacă ați găsit în mod corect la punctul de intersecție. Pentru acest substitut valoarea X în ecuația f (x) = 0.

Graful y = f (x) - este multimea tuturor punctelor din planul, coordonatele x, y satisfac relația y = f (x). grafic Funcția ilustrează comportamentul și proprietățile funcției. Pentru reprezentarea grafică mai multe valori, de obicei, selectate argument x și valorile corespunzătoare ale funcției y = f (x) sunt calculate pentru ele. Pentru mai multe comploturi precisă și vizuală este utilă pentru a găsi punctul de intersecție cu axele de coordonate.

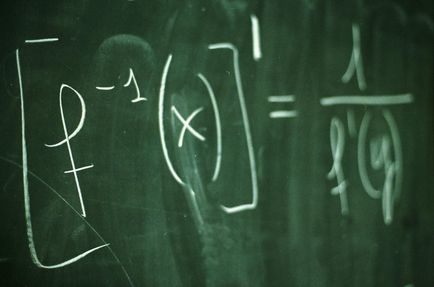
Pentru a găsi graficul punctului de intersecție cu axa y, este necesar să se calculeze valoarea funcției la x = 0, adică, găsi f (0). De exemplu, utilizarea unei funcții liniare grafic prezentat în Fig.1. Valoarea sa la x = 0 (y = a * 0 + b) este egal cu b, prin urmare, graficul intersectează axa ordonatei (axa Y), la un punct (0, b).

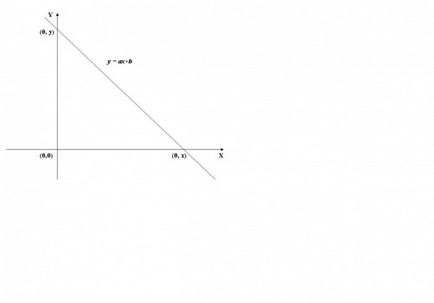
La trecerea abscisă (axa X), valoarea funcției este 0, adică, y = f (x) = 0. Pentru a calcula x trebuie să rezolve ecuația f (x) = 0. În cazul unei funcții liniare obținem ecuația ax + b = 0, din care am găsit x = -b / a.

Astfel, axa X intersectează un punct (-b / a, 0).

In cazuri mai complexe, de exemplu, în cazul dependenței pătratic y pe x, ecuația f (x) = 0 are deci două rădăcini abscisă se intersectează de două ori. În cazul unei funcții y periodice pe x, de exemplu y = sin (x), graficul ei are un număr infinit de puncte de intersecție cu axa X.

Pentru a verifica găsirea coordonatele graficului punctelor de intersecție ale axei X este necesară pentru a substitui valorile găsite pentru x în f expresie (x). Valoarea expresiei pentru fiecare dintre x calculate trebuie să fie 0.

Desigur, geometria școală știm că medianele unui triunghi se intersectează la un moment dat. Prin urmare, conversația ar trebui să se desfășoare pe punctul de intersecție. în loc de câteva puncte.

În primul rând, aveți nevoie pentru a discuta despre alegerea soluțiilor adecvate pentru problema sistemului de coordonate. În general, în problemele astfel o singură latură a triunghiului este plasat pe axa 0x, astfel încât un punct coincide cu originea. Deci, nu se îndepărtează de la general acceptate soluțiile canoane și de a face bine (vezi. Fig. 1). Metoda triunghiului de referință joacă un rol fundamental, deoarece este întotdeauna posibil să se meargă de la unul la altul (pe care o puteți vedea pentru viitor).

Lăsați triunghiul cerut definit de doi vectori de laturile sale AC și AB un (x1, y1) și b (x2, y2), funingine, respectiv. Mai mult decât atât, prin construcție, y1 = 0. Terțul corespunde Sun c = a-b, c (x1-x2, y1 -Y2), în conformitate cu această ilustrație. Punctul A este plasat la origine, adică coordonatele A (0, 0). De asemenea, este ușor de observat că în coordonatele (x2, y2), o C (x1, 0). Se poate concluziona că lucrarea unui triunghi a coincis doi vectori în mod automat cu trei puncte lui de locuri de muncă.

Următoarele este necesar pentru a termina triunghiul la dimensiunea corespunzătoare a ABDC paralelogramului. Este cunoscut faptul că punctul de intersecție al diagonalelor unui paralelogram, acestea sunt împărțite în jumătate, astfel încât AQ median al triunghiului ABC este coborât de la A la alta BC. Vectorul s include diagonală și mediana este, conform regulii paralelogramului suma geometrică a și b. Apoi, s = a + b, iar coordonatele sale s (x1 + x2, y1 + y2) = s (x1 + x2, y2). Aceste coordonate sunt aceleași și punctul D (x1 + x2, y2).

Acum putem trece la prepararea unei ecuații liniare cuprinzând s, mediana AQ si sa-mi mai important, punctul dorit de intersecție al medianelor H. Deoarece vectorul în sine este trimiterea s-conductiv pentru o anumită linie, iar punctul cunoscut A (0, 0) care îi aparțin, cel mai simplu - este de a utiliza o ecuație plan al unei linii în formă canonică: (x-x0) / m = (y-y0) /n.Zdes (x0, y0) coordonatele unui punct arbitrar al liniei (litera a (0, 0) ) și (m, n) - coordonatele s (vector (x1 + x2, y2) și astfel încât l1 linia dorită va avea forma: x / (x1 + x2) = y / y2 ..

Modul cel mai natural de a găsi coordonatele punctului - este definiția intersecția a două linii. Prin urmare, ar trebui să găsească o altă linie care conține t. N. În acest scop, Fig. 1 este realizat dintr-o altă construcție paralelogramului APBC diagonală este g = a + c = g (2x1-x2, Y2) cuprinde o a doua mediană CW, C coborâte din partea AB. Acesta cuprinde un punct diagonal C (x1, 0), coordonatele cărora va juca un rol (x0, y0) și vectorul de direcție este aici g (m, n) = g (2x1-x2, Y2). Prin urmare, l2 este dată de ecuația: (x-x1) / (2 x1-x2) = y / (- y2).

Rezolvarea ecuației împreună la L1 și L2, este ușor de a găsi coordonatele punctului de intersecție al medianelor H: H ((x1 + x1) / 3, y2 / 3).