Cum de a găsi punctul de intersecție cu axa x

Algebra dreptunghiular sistem de coordonate în planul format de două axe perpendiculare între ele - axa x (axa orizontală) și axa Y (axa verticală). punct de trecere - punctele în care graficele funcționale traversează axele. Punctul de intersecție cu axa Y și punctul de intersecție cu axa X situată pe axele respective. În probleme simple, cu punctul de intersecție al axei X este ușor de găsit pe funcția de program. De asemenea, punctul de intersecție poate fi calculată cu ajutorul ecuației.

pași Editare

Metoda 1 de la 3:
Folosind graficul functiei Edit

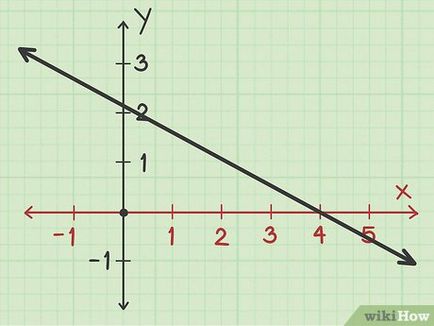
Ia sistem format din două axe de coordonate rectangulare axa X - axa X (axa orizontală care este direcționată de la stânga la dreapta) și axa Y (axa verticală care este îndreptată în sus). [1] Pentru a găsi un punct de intersecție cu axa X, să ia o privire la această axă.

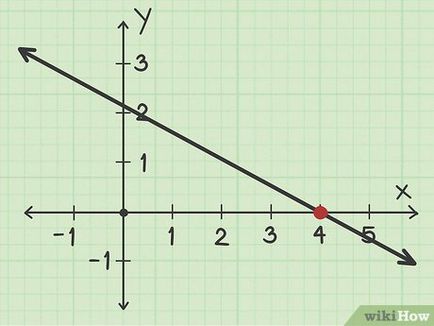
Localizați punctul în care graficul intersectează X. Punct de trecere Acest generat cu axa osiei X. [2] Dacă este necesar, pentru a găsi punctul de intersecție cu axa X a graficului poate coordona x din acest punct va fi un număr întreg, cum ar fi 4. Cu toate acestea, în majoritatea cazurilor, orarul va fi capabil să determine aproximative de coordonate x. de exemplu, între 4 și 5.

Se înregistrează coordonatele punctului de intersecție cu coordonatele punctului de axa X. sunt scrise ca o pereche de coordonate (x. Y). [3] Prima coordonată - este x coordonata punctului de intersecție cu axa X; a doua coordonate (coordonate y) este întotdeauna egal cu 0, deoarece punctul de intersecție cu axa X se află pe această axă. [4]

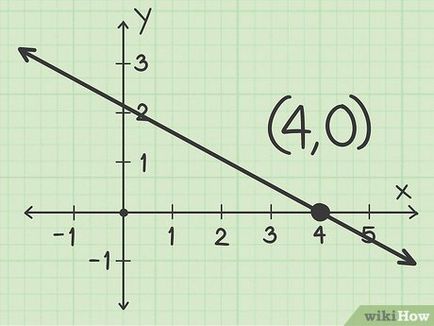
• De exemplu, dacă x coordonata punctului de intersecție este egal cu 4, perechea de coordonate ale unei intersecții cu coordonatele axelor X sunt (4. 0).

Determina dacă ecuația este scris sub forma unei ecuații liniare Diophantine. Această ecuație este de forma A + B x y = C. [5] în care A. B. C - sunt întregi, x și y - coordonatele unui punct care se află pe o linie dreaptă (ecuație liniară a graficului).

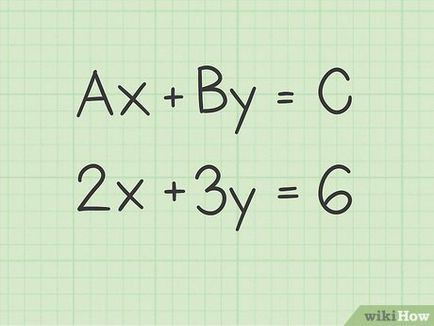
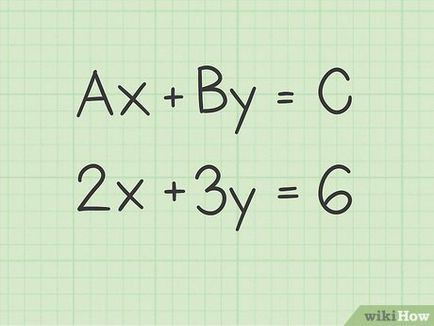
• De exemplu, având în vedere ecuația 2 x + 3, y = 6.

În schimb înlocuitor y 0. Punctul de intersecție cu axa X este punctul în care linia dreaptă intersectează această axă. [6] y-coordonata punctului de intersecție al liniei cu axa X este întotdeauna 0. [7] Prin urmare, pentru a găsi punctul de intersecție cu axa X, este necesar să se înlocuiască în locul y 0 și găsi valoarea lui x.

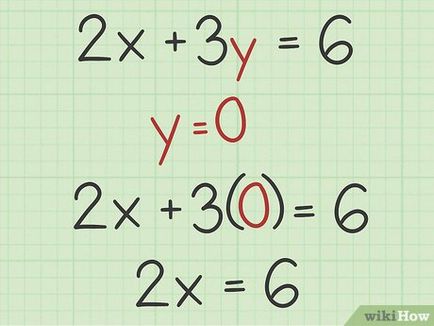
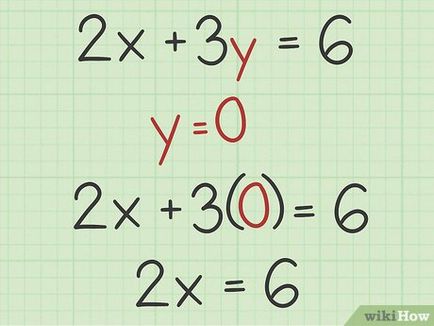
• În exemplul nostru, dacă în loc să înlocuim y 0, ecuația poate fi scrisă astfel: 2 x + 3 (0) = 6; Această ecuație este simplificată până la 2 x = 6.

Se înregistrează coordonatele punctului de intersecție cu coordonatele punctului de axa X. sunt scrise ca o pereche de coordonate (x. Y). Prima Coordonata - este Coordonata x. valoarea pe care tocmai l-ați găsit și a doua coordonată (coordonata y) este întotdeauna egal cu 0, deoarece punctul de intersecție cu axa X se află pe această axă. [8]

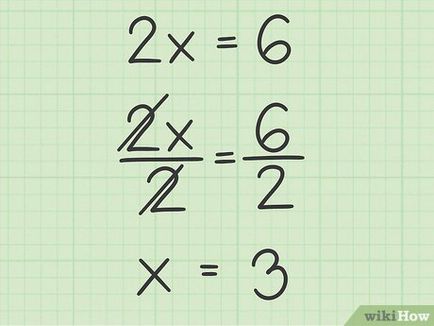
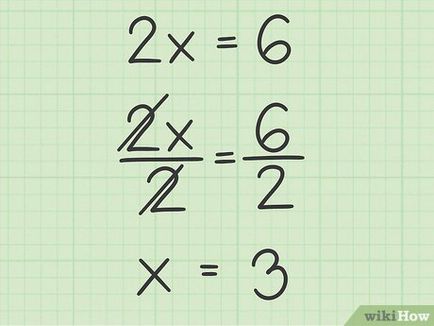
• De exemplu, graficul ecuației liniare 2 x + y = 3, 6 intersectează axa X la punctul cu coordonatele (3. 0).

Metoda 3 din 3:
Folosind formula de rezolvare a ecuației pătratice Edit

Determina dacă ecuația este scris sub forma unei ecuații pătratice. ecuația pătratică este de forma a x 2 + b x + c = 0 + bx + c = 0>. [9] Ecuația pătratică are două rădăcini ale unui astfel de grafic ecuație reprezintă parabolei intersectează axa X și două puncte. [10]

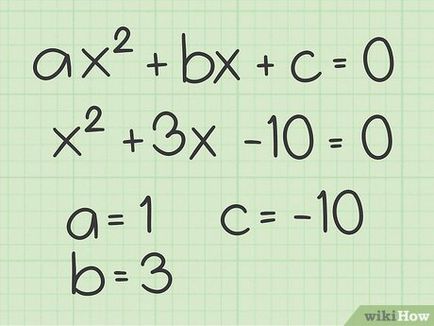
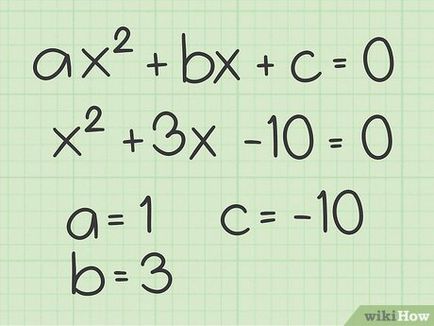
• De exemplu, ecuația x 2 + 3 x - 0 = 10 + 3x 10 = 0> este o ecuație pătratică, astfel încât graficul intersectează axa X în două puncte.

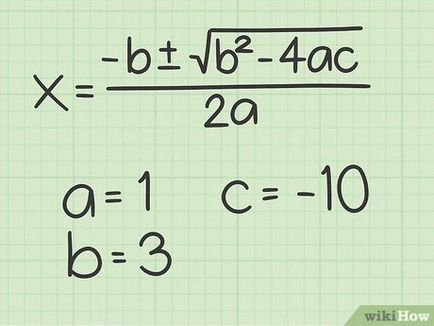
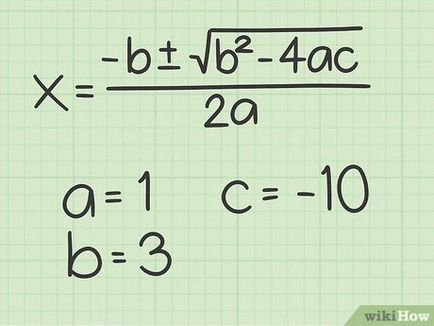
Notați formula pentru rezolvarea unei ecuații pătratică. Formula: x = - b ± b 2 - 4a c 2a >>>>> -4ac. în cazul în care un - coeficient al doilea ordin variabil (x 2>), b - coeficientul variabilei de ordinul întâi (x), c - termen constant. [11]

Valorile corespunzătoare de substituție în formula pentru a rezolva o ecuație pătratică. Asigurați-vă că fiecare variabilă se înlocuiește în loc de valoarea corectă.

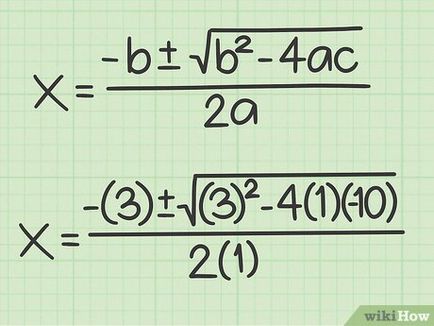
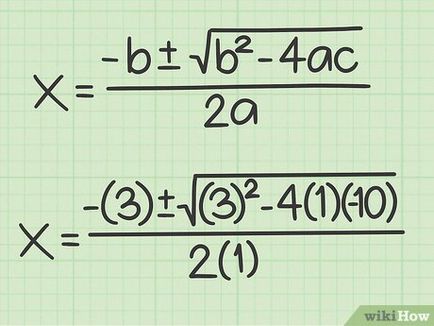
• De exemplu, dacă ecuația este x 3 + 2 x - 0 = 10 + 3x 10 = 0>. Formula este scris după cum urmează: x = - 3 2 ± 3 - 4 alineatul (1) (- 10) 2 (1) -4 (1) (- 10) >>>>>.

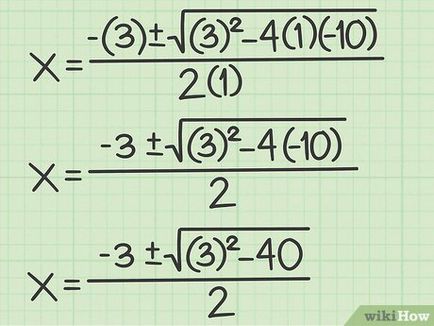
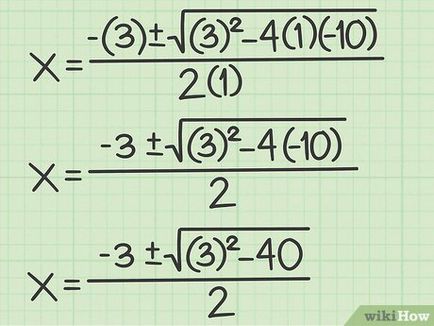
Regulamentul

• Ni se dă o ecuație liniară de forma y = k x + b. Trebuie să știm panta (este valoarea coeficientului k) și punctul de intersecție de coordonate „y“ a liniei drepte cu axa Y (care este egală cu valoarea coeficientului b). În loc de „în“ substitut 0 și localizați „x“. Vei primi o coordonată „x“ puncte de intersecție cu axa X

articole suplimentare

Cum se convertesc la mililitri de grame

Cum se calculează volumul cutiei

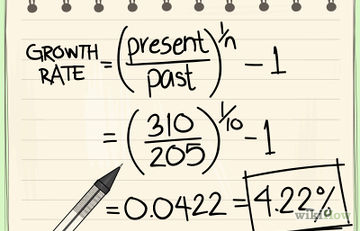
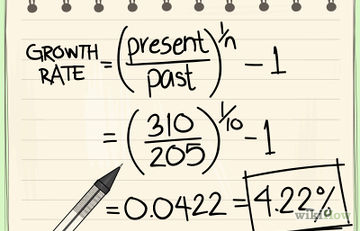
Cum de a calcula rata de creștere

Cum de a găsi rădăcina pătrată a unui număr manual

Cum de a calcula probabilitatea

Cum se calculează variația procentuală

Cum de a găsi domeniul funcției

Cum de a găsi un set de valori

Cum de a simplifica expresii algebrice

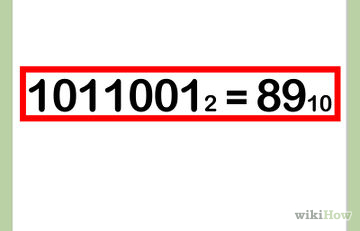
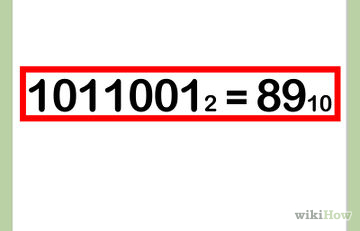
Cum se convertesc la binar în zecimal