Cum de a găsi raza cercului un triunghi

Cercul poate fi înscris de patrulater dacă a + c = b + d, unde a, b, c, d - patrulater laterală în ordine. În jurul circumferinței patrulaterului poate fi descrisă, în cazul în care opusul unghiurilor adăuga până la 180 de grade;

Pentru astfel de cercuri Triangle există întotdeauna.

Zona de căutare a triunghiului - una dintre cele mai comune sarcini ale geometriei plane școlar. Cunoașterea celor trei laturi ale unui triunghi este suficient pentru a determina zona de orice triunghi. In cazuri particulare, isoscel și triunghiuri echilaterale suficient pentru a cunoaște lungimea a două și, respectiv, de o parte.

• Lungimea laturilor triunghiurilor, formula lui Heron, teorema cosinusului

Fiind dat un triunghi ABC cu laturi AB = c, AC = b, BC = a. Suprafața unui astfel de triunghi poate fi găsit de formula Heron.

Perimetrul triunghiului P - este suma lungimilor celor trei laturi ale sale: P = a + b + c. Notăm-l semiperimetrul pentru p. Acesta va fi egal cu p = (a + b + c) / 2.

Formula lui Heron pentru zona triunghiului este după cum urmează: S = sqrt (p (p-a) (p-b) (p-c)). Dacă vopseaua semiperimetrul p, obținem: S = sqrt (((a + b + c) / 2) ((b + ca) / 2) ((a + cb) / 2) ((a + bc) / 2) ) = (sqrt ((a + b + c) (a + bc) (a + cb) (b + ca))) / 4.

Este posibil să se obțină o formulă pentru aria unui triunghi și alte considerente, de exemplu, folosind teorema cosinusului.

Conform teorema cosinusului AC ^ 2 = (AB ^ 2) + (BC ^ 2) -2 * AB * BC * cos (ABC). Folosind această notație, expresia poate fi scrisă sub forma: b ^ 2 = (a ^ 2) + (c ^ 2) -2a * c * cos (ABC). De aici, cos (ABC) = ((a ^ 2) + (c ^ 2) - (b ^ 2)) / (2 * a * c)

Aria triunghiului este, de asemenea, în conformitate cu formula S = a * c * sin (ABC) / 2, prin cele două părți și un unghi între ele. Unghiul Sinus ABC poate fi exprimată prin cosinusul folosind identități trigonometrice de bază :. Sin (ABC) = sqrt (1 - ((cos (ABC)) ^ 2) Înlocuind formula sine pentru zona și scriere poate ajunge la o formulă pentru zona ABC.

Cele trei puncte definesc în mod unic un triunghi în sistemul de coordonate cartezian - este partea superioară. Cunoscând poziția lor în raport cu fiecare dintre axele de coordonate pot fi calculate orice parametri ai figurii plane delimitate de și incluzând perimetrul zonei sale. Acest lucru se poate face în mai multe moduri.

Utilizați formula lui Heron pentru calculul ariei unui triunghi. Acesta a implicat dimensiunea a trei laturi ale figurii, astfel încât calculele de la definiția lor. Lungimea fiecărei părți trebuie să fie egală cu rădăcina pătrată a sumei pătratelor lungimilor proiecțiilor sale pe axele. Dacă notăm coordonatele vârfurilor A (X₁, Y₁, Z₁), B (X₂, Y₂, Z₂) și C (X₃, Y₃, Z₃), lungimile laturilor lor pot fi exprimate ca: AB = √ ((X₁-X₂) ² + ( Y₁-Y₂) ² + (Z₁-Z₂) ²), BC = √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²), AC = √ ((X₁-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).

Pentru a simplifica calculele, introduceți variabila auxiliară - semiperimetrul (P). După cum sugerează și numele, este jumatate din suma lungimilor tuturor părților: P = ½ * (AB + BC + AC) = ½ * (√ ((X₁-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ²) + √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²) + √ ((X₁-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).

Se calculează aria (S) cu formula Heron - elimina semiperimetrul rădăcină al produsului prin diferența dintre acesta și lungimea fiecărei laturi. În forma sa generală poate fi scrisă astfel: S = √ (P * (P-AB) * (P-BC) * (P-AC)) = √ (P * (P-√ ((X₁-X₂) ² + ( Y₁-Y₂) ² + (Z₁-Z₂) ²)) * (P-√ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²)) * (P-√ ((X₁ -X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²)).

Câmpurile de formular menționa separat fiecare coordonată a fiecăruia dintre vârfurile triunghiului - acestea sunt denumite aici ca Ax, Ay, Az, etc. Dacă triunghiul este dat coordonatele bidimensionale în domeniul z - Az, Bz și cz - scrie la zero. În „Precizia de calcul“, a seta numărul dorit de zecimale, făcând clic pe pictograma mouse-ului, plus sau minus. Plasat sub forma unei portocale „calculează“ buton pentru a presa nu este necesar, calculele se vor face fără ea. Răspunsul vă va găsi lângă „zona de triunghi“ - este situat chiar sub butonul portocaliu.

• găsi zona triunghiului cu noduri

Uneori, în jurul unui poligon convex poate desena un cerc, astfel încât vârfurile tuturor unghiurilor culcat pe ea. este necesar să numim astfel un cerc cu privire la poligon descris. Centrul său nu trebuie să fie înscrisă în perimetrul figurii, dar utilizând proprietățile cercului circumscris. găsi acest punct nu este de obicei foarte dificil.

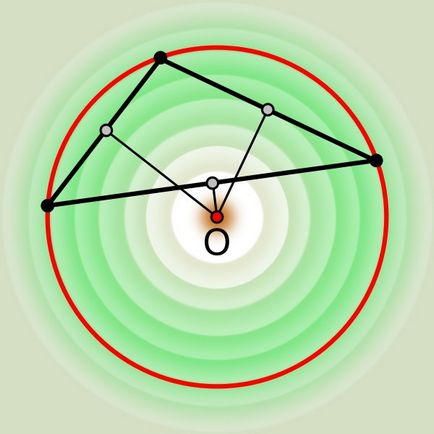
• Riglă, creion, echer sau un set pătrat, busole.

În cazul în care un poligon, despre care doriți să descrie un cerc, elaborat pe suport de hârtie, pentru a găsi centrul cercului și suficient de linie, un creion și un echer sau un poligon. Se măsoară lungimea oricare dintre cifrele părților, determină mijlocul ei și a pus în locul punctului auxiliar de desen. Cu poligon sau în interiorul diapozitiv poligon echer perpendicular pe acea parte a segmentului la intersecția cu partea opusă.

Efectuați aceeași operație cu orice alt poligon parte. Intersecția a două segmente construite va fi punctul dorit. Acest lucru rezultă din proprietățile de bază ale cercului circumscris - centrul unui poligon convex cu orice număr de laturi se află întotdeauna la midperpendiculars intersecție a avut loc la aceste părți.

Pentru definirea poligoane regulate cerc înscris, iar centrul poate fi mult mai ușor. De exemplu, în cazul în care acesta este un pătrat, apoi trage două diagonale - și intersecția lor este centrul cercului inscris st. In orice poligon regulat cu un număr par de laturi suficiente pentru a conecta două perechi de segmente auxiliare situate vizavi una față de alte unghiuri - centrul cercului circumscris trebuie să coincidă cu punctul de intersecție a acestora. Într-un triunghi dreptunghic pentru a rezolva problema specifică pur și simplu mijlocul celei mai lungi laturi a figurii - ipotenuzei.

Dacă o condiție nu se cunoaște dacă este posibil, în principiu, să atragă cercul circumscris pentru un anumit poligon, după determinarea punctului central dorit și oricare dintre următoarele metode pe care le puteți afla. Pune pe distanța busola între punctul de găsit și oricare dintre nodurile din separatoare set tsentrokruzhnosti putative și desena cerc - fiecare nod ar trebui să revină pe acest cerc. Dacă nu este, atunci, nu una dintre principalele caracteristici și descrie un cerc în jurul acestui poligon nu se poate.

Uneori, în viață trebuie să ne confruntăm cu situații care necesită cunoștințe de geometrie. Astfel de informații sunt rareori folosite în viața de zi cu zi, atât de uitat. Una dintre cele mai populare întrebări este de a găsi aria unui triunghi prin intermediul celor două părți.

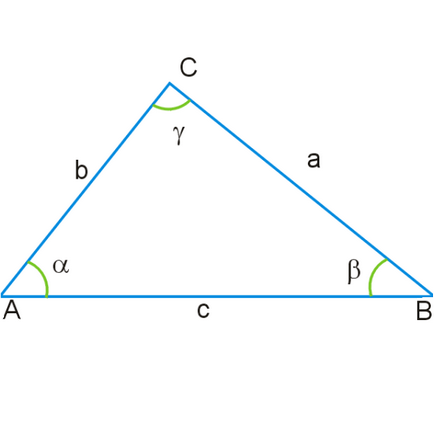
Aria triunghiului, care se calculează în funcție de lungimea celor două laturi, necesită măsurarea și unghiul dintre ele. Pentru a face acest lucru, utilizați un echer sau alte instrumente speciale. De exemplu, conice - foarte convenabil pentru măsurarea unghiurilor în cameră.

Odată ce ați găsit dimensiunea triunghiului două părți și unghiul dintre ele, du-te la calcule. Găsirea zonei urmează următoarea formulă: SΔ abc = 1/2 ab unghi păcat. În același timp, dacă aveți unghiul drept în triunghiul dintre cele două părți cunoscute, cu formula poate fi redusă: SΔ abc = 1/2 ab.

Pentru a calcula sinusul unghiului, puteți utiliza tabelul trigonometrice Bradis, care oferă valorile pentru dimensiunile cele mai uzuale ale unghiurilor. O altă modalitate buna de a calcula sinusul unghiului este calculatorul. În fiecare din sistemul de operare Windows este printre programele standard. Deschideți-l și comută la „Inginerie“, care este în secțiunea „View“. Apoi introduceți mărimea unghiului, sinusul pe care doriți să calculeze. Apoi selectați unitățile pentru răspunsul calculat. Acesta poate fi de grade, radiani, sau excitat. Puteți face acest lucru folosind butoanele de mai jos câmpul de introducere. Apăsați «păcat» și pentru a obține rezultatul.

Desigur, sinusul unghiului poate fi acum calculat cu ajutorul diverselor calculatoare on-line avansate cu o interfață prietenoasă și mai multe caracteristici. Găsiți un astfel de program pe internet nu este dificil, pentru că au oferit foarte mult. Pur și simplu introduceți în motorul de căutare „funcții calculator trigonometrice“.

Acum, înmulțind ambele părți ale unui triunghi de lungime și sinusul unghiului dintre ele, se împarte la 2 și gata să răspundă. zonă a unui triunghi este găsit.