Cum de a verifica dacă un număr este prim

Primes - numere care sunt divizibile numai de ei înșiși și 1; Toate celelalte numere sunt numite numere compuse. Există mai multe modalități de a determina dacă un număr este prim. Unele metode sunt relativ simple, dar ele nu sunt potrivite pentru un număr mare. Alte metode utile pentru un număr mare reprezintă de fapt algoritmi probabilistici, care sunt uneori greșit caracterizate ca un număr de simplu sau compozit.

pași Editare

Metoda 1 de la 4:
separatoare Bust Editare

divizoare Bust - cel mai simplu mod de a determina ușurința. În cazul unui număr mic, este, poate, de asemenea, cel mai rapid mod. Aceasta se bazează pe definirea unui număr prim: numărul este prim dacă nu are nici o alta decât el însuși și un divizori.

Fie n - numărul care urmează să fie testat. Conform acestei metode, trebuie să împărțiți numărul n pentru toate posibile separatoare întregi. Pentru valori mari ale lui n, de exemplu, n = 101, verificând fiecare separator ia o mulțime de timp. Dar există modalități de a reduce numărul de separatoare pe care doriți să le verificați.

Decideți dacă numărul n este chiar. Orice număr par este divizibil cu 2. În cazul în care întreg n - chiar, atunci puteți declara imediat că nu este un simplu (care este, este un număr întreg). Pentru o determinare rapidă a parității să acorde o atenție la ultima cifră. În cazul în care ultima cifră de 2, 4, 6, 8,0, că numărul este chiar și nu este ușor.

• Singura excepție de la această regulă - numărul 2. Deci, este divizibil doar de la sine și 1, numărul 2 - un număr prim. Astfel, numărul 2 este singurul număr prim impar.

Divizare n pentru fiecare număr întreg de la 2 la n-1. Deoarece divizorul este mai mică decât dividendul, verificarea tuturor divizori mai puțin decât n și mai mare de 2 ar trebui să arate dacă n prim. Începi cu un număr mai mare de 2, deoarece chiar și numere (care sunt multipli de 2), nu sunt numere prime. Acest lucru nu este cel mai eficient mod de testare primality, dar există o serie de metode de testare de optimizare.

• De exemplu, a verifica numărul 11. În acest caz, diviza (uniform) 11 3, 4, 5, 6, 7, 8, 9, 10. Deoarece nici unul dintre aceste numere nu diviza (uniform) 11, numărul 11 ​​- simplu număr.

Pentru a economisi timp, verificați separatoare la valoarea rotunjită rădăcină pătrată (n). Verificați toate divizori de la 2 la n-1 poate fi consumatoare de timp. De exemplu, dacă doriți să verificați numărul de 103, atunci trebuie să testați următoarele separatoare: 3, 4, 5, 6, 7, și așa mai departe până la 102! Dar acest lucru poate fi evitat - trebuie doar să verificați separatoare între 2 și rotunjită rădăcină pătrată (n).

• Explicația acestui principiu. Luați în considerare multiplicatori 100. 100 = 100 x 1, 2 x 50 4 x 25 5 x 20, 10 x 10, 20 x 5 x 25 4 2 x 50, 100 x 1. De notat că după perechea de multiplicatori 10 × 10 toate perechile de multiplicatori sunt repetate (doar factorii din aceste perechi sunt schimbate). Prin urmare, puteți ignora divizorii lui n este mai mare decât rădăcina pătrată a (n).
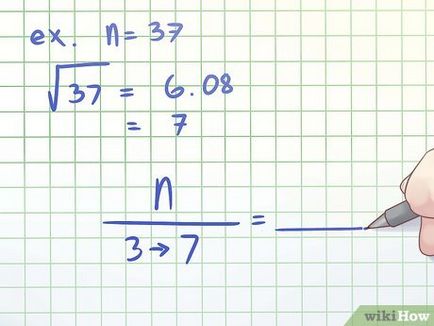
• De exemplu, n = 37. verificare nu este necesar pentru a testa toate divizorii de la 3 la 36. In schimb, separatoare de verificare între 2 și valoarea rotunjită a rădăcinii pătrate (37).
  • Rădăcina pătrată (37) = 6,08. Runda acest număr la 7.
  • 37 nu este divizibil cu 3, 4, 5, 6, 7, deci - simplu.

Pentru a economisi și mai mult timp, testați numai divizori prime. Prin definiție, orice număr compozit poate fi exprimată ca produsul a două sau mai multe numere prime. Prin urmare, numărul n diviziune pentru divizor integrală - operațiune se repetă de prisos diviziunea n în prim divizori. Astfel, puteți restrânge și mai mult seria de teste separatoare.

• Acest lucru înseamnă că toate divizorii chiar și toate divizori de care sunt multipli de numere prime pot fi omise.
• De exemplu, a verifica numărul 103. rădăcină pătrată din 103 este rotunjită la 11. separatoare simple 2 și 11 este de 3, 5, 7, 11. Divizoare 4, 6, 8, 9, 10 pot fi omise (9 multiplu de 3, și toate celelalte separatoare - chiar numere). Astfel, ați redus numărul de separatoare de testare la patru numere.
  • Divizoarele 3, 5, 7, 11 nu împărtășesc (uniform) numărul de 103, deci - simplu.