Curbura și raza de curbură

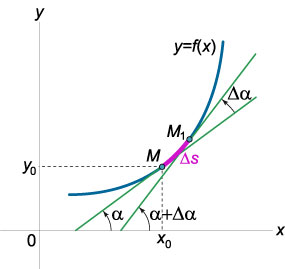
Să considerăm o curbă plan definit de ecuația \ (y = f \ stânga (x \ dreapta). \) Să presupunem că la punctul \ (M \ stânga (\ dreapta) \) a avut loc tangente la această curbă, care formează un unghi \ (\ alpha \) cu axa orizontală (Figura \ (1 \)). La deplasarea \ (\ Delta s \) de-a lungul unui arc de punct curbă \ (M \) se deplasează la punctul \ (\) Poziția tangentei este de asemenea schimbat:. Unghiul de înclinare a tangentei la axa \ (Ox \) la punctul \ (\) va fie \ (\ alpha + \ Delta \ alpha. \) Prin urmare, atunci când (\ Delta s \) deplasarea punctului curbei la distanță \ tangentă rotește \ (\ Delta \ alpha. \) (Vom presupune că unghiul \ ( \ alpha \) crește cu rotire în sens antiorar.)

Valoarea absolută a raportului de \ (\ mare \ frac >> \ normalsize \) se numește curbura medie a arcului \ (M. \) În limita, cu \ (\ Delta s \ la 0 \), obținem curbura curbei la punctul \ (M: \) \ [K = \ lim \ limits_ \ din stânga | >>> \ dreapta |. \] din această definiție rezultă că curbura în orice punct al curbei caracterizează viteza de rotație a tangentei la acest punct.

Pentru o curbă plană \ (y = f \ stânga (x \ dreapta) \) curbură la punctul \ (M \ stânga (\ dreapta) \) se exprimă prin primul și al doilea derivatele funcției \ (f \ left (x \ dreapta) \) formula \ [K = \ frac \ dreapta | >> \ dreapta)> ^ 2 >> \ right]> ^ \ normalsize >>>> \] Dacă curba este dată în ecuațiile parametrice de forma \ (x = x \ stânga (. t \ dreapta), \) \ (y = y \ stânga (t \ dreapta), \) este curbura în orice punct \ (M \ stânga (\ dreapta) \) este egal cu \ [K = \ frac \ dreapta |> > \ dreapta)> ^ 2> + \ dreapta)> ^ 2 >> \ right]> ^ \ normalsize >>>>. \] în cazul în care curba este dată polară ecuația \ (r = r \ stânga (\ theta \ dreapta), \) curbura este dată de \ [K = \ + 2 \ dreapta)> ^ 2> Frac - rr ''> \ dreapta | >> + \ dreapta)> ^ 2 >> \ right]> ^ \ normalsize >>>>. \] raza de curbură a curbei, la \ (M \ stânga (\ dreapta) \) se numește curbură inversă \ (K \) curba dată în punctul dat: [. R = \ frac \] \ consecință, curbele plane având în vedere ecuația explicită \ (y = f \ stânga (x \ dreapta), \) raza curbura la punctul \ (M \ stânga (\ dreapta) \) să fie dată de expresia \ [R = \ frac \ dreapta)> ^ 2 >> \ right]> ^ \ normalsize >>>> \ dreapta | >> \].

Calculați curbura elipsei \ [\ frac >>>> + \ Frac >>>> = 1 \] la nodurile sale.

Evident, este suficient să se găsească curbura elipsă la puncte \ (A \ stânga (\ dreapta) \) și \ (B \ stânga (\ dreapta) \) (Figura \ (2 \)), deoarece datorită simetriei curbura curbei în două vârfuri opuse elipsă va fi la fel.

Pentru a calcula curbura este convenabil să se miște din ecuația canonică elipsă ecuației în formă parametrică. \ [X = o \ cos t, \; \; \; y = b \ păcatul t \.] Unde \ (t \) - un parametru. La punctul \ (A \ stânga (\ dreapta) \) parametru este setat la \ (t = 0, \) și la punctul \ (B \ stânga (\ dreapta) \) valoarea sa este \ (t = \ mare \ frac \ normalsize. \)

Găsiți curbura și raza de curbură a parabolei \ (y = \) la origine.

Găsiți curbura și raza de curbură a curbei \ (y = \ cos mx \), la punctul maxim.

Această funcție atinge un maxim la punctele \ (x = \ mare \ frac> \ normalsize, \ n \ în Z. \) Prin periodicitatea curbură în toate punctele maxime identice, deci este suficient să se ia în considerare numai punctul \ (x = 0 \).