Derivata, și introducerea definiției din clasa a 10-a, în algebra
Ce vom învăța:
1. Introducere în conceptul de derivat.
2. Un pic de istorie.
3. Definiția derivat.
4. Funcția derivat pe grafic. semnificația geometrică a derivatului.
5. Algoritmul pentru găsirea funcția derivată.
6. Diferențierea funcțiilor.
7. Exemple.
Introducerea conceptului de derivat
Există mai multe sarcini foarte diferite, în sens, dar există modele matematice care ne permit sa numaram obiectivele noastre exact în același mod. De exemplu, dacă luăm în considerare astfel de sarcini ca:
a) Există un anumit cont bancar, care se schimbă în mod constant la fiecare câteva zile, suma este în continuă creștere, este necesar pentru a găsi viteza cu care crește cheltuielile.
b) Planta produce bomboane, bomboane este o creștere constantă a producției, pentru a găsi cât de rapid tot mai mare de creștere de bomboane de ciocolată.
c) Viteza vehiculului la un anumit moment t, dacă se cunoaște poziția vehiculului și se deplasează într-o linie dreaptă.
d) Vom programa funcția dată și un punct de tangenta a avut loc la aceasta, este necesar pentru a găsi panta unei tangenta.
Formularea obiectivelor noastre sunt destul de diferite, și se pare că acestea sunt rezolvate moduri complet diferite, dar matematica pentru a descoperi cum puteți rezolva toate aceste probleme în exact același fel. conceptul de derivat a fost introdus.
Un pic de istorie
Derivatul Termenul este introdus mare matematician - J. Lagrange, tradus în limba română este derivat din cuvântul derivee francez, el a introdus, de asemenea, notația modernă a derivatului care vor fi luate în considerare mai târziu.
Considerat conceptul de derivat în lucrările lui Leibniz și Newton, folosirea termenului acestea sunt în geometrie și mecanică, respectiv.
Puțin mai târziu, vom afla ce un derivat este determinat de limita, dar există o ușoară paradox în istoria matematicii. Matematicienii au învățat să numere derivat înainte de a introdus conceptul de limită și să înțeleagă de fapt ceea ce este un derivat.
definiția unui derivat
Lăsați funcția y = f (x) este definit pe un anumit interval de timp, care conține în interiorul său un x0 punct. Argumentul increment Ax - nu iese din gama noastră. Gasim increment Dy și formează raportul Dy / Ax, dacă limita acestui raport când Ax tinde la zero, limita specificată se numește derivata funcției y = f (x) la x0 și notat f „(x0).
Să încercăm să explicăm ce este un derivat care nu este din punct de vedere matematic:
Într-un limbaj matematic: derivat - limită a raportului funcției creștere contribuind la creșterea argumentului său tinde la zero creștere a argumentului.
În limbajul obișnuit: derivat - funcționează rata de schimbare în punctul x0.
Să ne uităm la graficele de trei funcții:
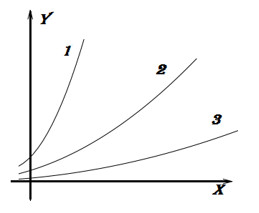
Băieți, ce crezi, care a curbelor este în creștere mai rapidă?
Răspunsul pare a fi evident pentru toți 1, curba este în creștere mai rapid decât ceilalți. Ne uitam la cat de cool merge în sus graficul funcției. Cu alte cuvinte - cât de repede se schimbă atunci când schimbați ordonata x. Una și aceeași funcție în locații diferite pot avea o valoare diferită a derivatului - adică, se poate schimba mai repede sau mai lent.
Funcția derivat pe grafic. semnificația geometrică a derivatului
Acum, să vedem cum să găsească derivatul folosind graficele:
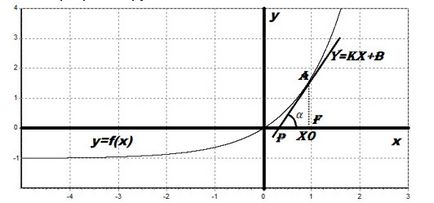
Să ne uităm la funcțiile noastre de program: Desenați la X0 c abscisa tangenta la graficul funcției. Tangentă și programul funcției noastre în contact de la punctul A. Trebuie să evalueze modul în care merge abrupt grafic al funcției. O valoare convenabilă pentru aceasta - panta tangentei.
Definiția. Derivata funcției în punctul x0 este egal cu panta tangentei la graficul funcției în acel punct.
Unghiul de înclinare a tangentei este ales ca unghiul dintre tangenta și direcția pozitivă a axei x.
Deci, derivata funcției noastre este egal cu:
Și astfel derivatul de la X0 este panta tangentei este sensul geometric al derivatului.
Algoritmul pentru găsirea funcției derivat
Algoritmul pentru găsirea funcției derivatului y = f (x).
a) Pentru a fixa valoarea lui x, pentru a găsi f (x).
b) Găsiți incrementarea argumentului x + Ax, iar funcția valorii creștere a f (x + Ax).
c) Găsiți increment Dy = f (x + Ax) -f (x) funcția.
d) Creare relație: Dy / Ax
d) Se calculează
- este un derivat al funcției noastre.
diferențierea funcțiilor
Dacă funcția y = f (x) este derivata de la punctul x, atunci aceasta se numește diferențiabilă în punctul x. Procesul de diferențiere numită funcția derivatului y = f (x).
Să ne întoarcem la problema continuității funcției. Dacă funcția este diferențiabilă la un moment dat, atunci graficul funcției de la acest punct, puteți desena o funcție tangentă nu poate avea o pauză de la acest punct, atunci pur și simplu, pur și simplu nu se poate trage o tangentă.
Și astfel încât să putem scrie de mai sus a spus ca definiția:
Definiția. Dacă funcția este diferențiabilă la un punct x, atunci este continuă, în acest moment.
Cu toate acestea, în cazul în care funcția este continuă la un punct, aceasta nu înseamnă că este diferențiabilă în acest moment. De exemplu, funcția y = | x | x = 0 este continuu, dar nu poate deține o tangentă, și, prin urmare, derivatul nu există.
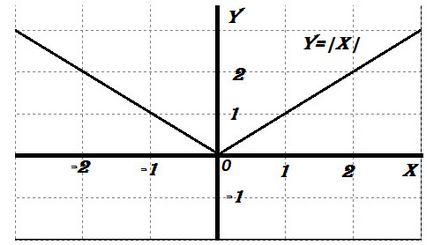
exemple ale derivatului
Găsiți derivata funcției: y = 3x
soluţie:
Vom folosi căutarea algoritmul derivate.
1) Pentru o valoare fixă de x, valoarea funcției y = 3x
2) La punctul x + Ax, y = f (x + Ax) = 3 (x + Ax) = 3x + 3 Ax
3) Găsiți funcția increment: Dy = f (x + Ax) -f (x) = 3x + 3 = 3x-Ax 3Δx
4) formează relația:
5) Găsiți limita:
Răspuns: f „(x) = 3
Găsiți derivata funcției y = 5x 2
soluţie:
Vom folosi căutarea algoritmul derivate.
1) Pentru o valoare fixă de x, valoarea funcției y = 5x 2
2) La punctul x + Ax y = f (x + Ax) = 5 (x + Ax) ^ 2 = 5 (x 2 + 2xΔx + 2 Ax)
3) Găsiți incrementul funcției:
Dy = f (x + Ax) -f (x) = 5x 2 + 10xΔx + 5Δx -5x 2 2 = 10xΔx + 5Δx 2
4) formează relația:
Găsiți derivatul de y = 2x 2 -x + 1
Vom folosi căutarea algoritmul derivate.
1) Pentru o valoare fixă de x, valoarea funcției
2) La punctul x + Ax y = f (x + Ax) = 2 (x + Ax) 2 - (x + Ax) + 1 = 2 (x 2 + 2xΔx + Ax 2) - (x + Ax) +1
Gasim funcția increment: Dy = f (x + Ax) -f (x) = = 2x 2 + 4xΔx + 5Δx 2 - (x + Ax) + 1-2x 2 + x-1 = = 4xΔx + 5Δx 2 -Δx
3) formează relația: