Despre operațiunile de biți

În acest articol vă voi spune cum să opereze operațiunile de biți. La prima vedere, ele pot părea oarecum complicat și inutil, dar de fapt nu este așa. In aceasta voi încerca să vă convingă.
Operatorii la nivel de bit efectuează operațiuni direct pe numere de biți, astfel încât numărul de exemple vor fi în sistem binar.
Voi vorbi despre următorii operatori la nivel de bit:
- | (OR la nivel de bit (OR)),
- (AND la nivel de bit (AND)),
- ^ (SAU exclusiv (XOR)),
Bit operațiuni sunt studiate în matematică discrete, precum și forma baza tehnologiei digitale, deoarece au stabilit logica de porți logice - elementele de bază ale circuitelor digitale. În matematică discrete, precum și în tehnologia digitală, tabelul de adevăr folosit pentru a descrie munca lor. Tabela de adevăr, mi se pare, mult mai ușor de înțelegere a operațiunilor de biți, așa că îi voi aduce în acest articol. Ele sunt, cu toate acestea, aproape niciodată folosit în explicațiile operatorilor la nivel de bit de limbaje de programare de nivel înalt.
Despre operatori la nivel de bit, de asemenea, trebuie să știți:
- Unii dintre operatorii de biti sunt similare cu declarații cu care s-ar putea să fie familiarizat cu (, ||). Acest lucru se datorează faptului că acestea sunt de fapt oarecum similare. Cu toate acestea, pentru a le confunda, în orice caz imposibil.
- Cele mai multe dintre operațiunile de biți sunt de atribuire compus operații.
Bitwise SAU (OR)
Bitwise OR operează un SAU logic echivalent, dar care se aplică fiecărei perechi de biți ai numărului binar. Rezultatul Bit este 0 numai dacă ambele biți corespunzătoare la 0. În toate celelalte cazuri, rezultatul binar este egal cu 1. Aceasta este, dacă avem următorul tabel de adevăr:
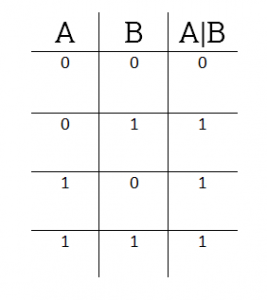
38 | 53 va fi:
Ca rezultat, vom obține 1001002. sau 3610.
Cu ajutorul operatorului bitmap și puteți verifica dacă un număr este par sau impar. Pentru numere întregi, în cazul în care LSB este 1, numărul impar (bazat pe conversia binar în zecimal). De ce face acest lucru dacă puteți utiliza doar 2%. Pe calculatorul meu, de exemplu, 1 se realizează cu 66% mai repede. îmbunătățire destul de bună performanță, vă spun.
OR exclusiv (XOR)
Diferența dintre SAU exclusiv și OR la nivel de bit, care timp de 1 doar un bit în pereche poate fi de 1:
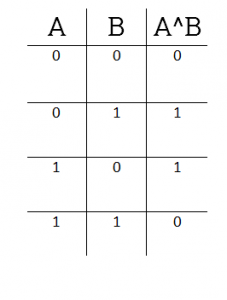
De exemplu, expresia 43 ^ 138 este același ...
Rezultatul va fi 20310
Când se folosește semnul bitwise negarea rezultatul va fi întotdeauna opusă numărul inițial (atunci când se lucrează cu numere semnate). De ce se întâmplă acest lucru, te invata acum.
cod suplimentar
Aici, ar trebui să-ți spun un pic despre procesul de reprezentare a numerelor întregi negative, în calculator, și anume codul suplimentar (complement față de doi). Fără a intra în detalii, este necesar pentru a facilita numerele binare aritmetice.
Principalul lucru pe care trebuie să știți despre numerele înregistrate în codul suplimentar - este faptul că MSB este semnul. În cazul în care este 0, atunci numărul este pozitiv, și coincide cu reprezentarea acestui număr în codul direct, în cazul în care 1 - este negativ. Asta este, 10111101 - număr negativ, și 01000011 - pozitiv.
(Utilizați negarea bitwise a ceea ce este, de fapt), pentru a converti un număr negativ în codul suplimentar necesar pentru a inversa toate biții de numărul și se adaugă 1 la rezultat.
De exemplu, dacă avem 109:
O caracteristică interesantă spre stânga prin poziția de deplasare N este că aceasta este echivalentă cu înmulțirea numărului de 2 N. Astfel, 43<<4 == 43*Math.pow(2,4). Использование сдвига влево вместо Math.pow обеспечит неплохой прирост производительности.
deplasare dreapta bitwise
După cum s-ar putea ghici, >> Deplasează biți pentru numărul de biți desemnat la dreapta.
Dacă operandul este pozitiv, spațiile goale sunt umplute cu zerouri. Dacă inițial lucrăm cu un număr negativ, atunci toate spațiile goale rămase sunt ocupate de unități. Acest lucru se face pentru a păstra caracterul în conformitate cu un cod suplimentar, a explicat mai devreme.
Deoarece o schimbare bitwise spre dreapta - aceasta este o opusă operație la trecerea de biți la stânga, este ușor de ghicit că numărul de deplasare dreapta în funcție de numărul N de poziție și împarte acest număr de 2 N. Din nou, acest lucru este mult mai rapid decât diviziunea convențională.
Deci, acum știi mai multe despre operațiunile și nu se tem de ele. Presupun că nu va utiliza >> 1 la fiecare diviziune de 2. Cu toate acestea, operațiunea de biți fi frumos să aibă în arsenalul dvs., iar acum le puteți folosi în caz de nevoie, sau pentru a răspunde la o întrebare delicată în interviu.