ecuații liniare

Numărul de rădăcini, indiferent de a și b:

- Când a = b = 0. aceasta înseamnă că ecuația are un număr nelimitat de soluții de la.

- Când a = 0. b ≠ 0. înseamnă că ecuația nu are rădăcini ca.

- Atunci când un ≠ 0. înseamnă că ecuația are o singură rădăcină.

ecuație liniară cu două variabile.

Ecuația variabilă x este egal tip A (x) = B (x). unde A (x) și B (x) - expresii ale lui x. Atunci când înlocuind valorile mulțimii T x în ecuație obținem adevărata egalitate numerică, care se numește un set de adevăr sau soluția acestei ecuații date ecuație. și toate astfel de valoare variabilă - rădăcinile ecuației.

Linear Ecuații 2 variabile sunt de forma:

- într-o formă generală: ax + de + c = 0,

- în formă canonică: ax + de = -c,

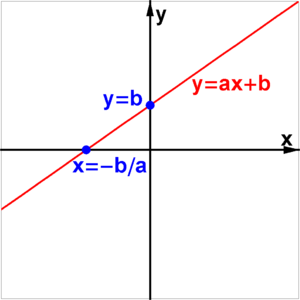
- sub forma unei funcții liniare: y = kx + m. în cazul în care.

Decizia sau rădăcinile ecuației este o pereche de valori variabile (x; y). care îl transformă într-o identitate. Aceste soluții de (rădăcini) ale ecuației liniare cu 2 număr nelimitat de variabile. Modelul geometric (grafic) al unei ecuații y directe = kx + m.

Dacă ecuația este pătrat X, atunci această ecuație se numește o ecuație pătratică.