formulele de reducere

Formulele de reducere. Acestea se referă la secțiunea „trigonometrie“ în matematică. Esența lor este de a aduce funcțiile trigonometrice ale unghiurilor într-o formă „simplă“. Importanța cunoașterii este posibil să se scrie mult. Aceste formule ca de mult 32 de bucăți!

Dacă aduceți cu formule nu sunt familiarizați, simplitatea lor de ieșire vă va încânta - există o „lege“ cu care este ușor de făcut. Și oricare dintre cele 32 de formule pe care scrie timp de 5 secunde.

Sunt doar câteva sarcini care va fi pe examen la matematică, în cazul în care, fără cunoașterea acestor formule au o șansă bună de a veni la durere în decizie. De exemplu:

- obiective pentru soluția unui triunghi dreptunghic, în cazul în care vorbim despre unghiul exterior, și sarcini pe colturile interioare ale unora dintre aceste formule sunt, de asemenea, necesare.

- sarcina de calcul a valorilor expresiilor trigonometrice; conversie numerică expresii trigonometrice; de conversie expresii trigonometrice alfabetice.

- obiectivele pentru tangenta și semnificația geometrică a tangentei necesită formula de reducere pentru tangenta, precum și alte sarcini.

- sarcini stereometrice timpul nu rareori necesară determinarea sinusul sau cosinusul unui unghi care variază de la 90 la 180 de grade soluțiile.

Și este doar acele aspecte care se referă la examenul. Și în cursul algebra este un set de sarcini, soluția care, fără cunoașterea formulelor de reducere pur și simplu nu pot face.

Deci, ce este la ceea ce este stipulat formula si cum o face mai ușor pentru rezolvarea problemelor?

De exemplu, aveți nevoie pentru a defini sinus, cosinus, tangenta, sau cotangentă orice unghi de la 0 la 450 de grade:

Unghiul alfa se află între 0 și 90 grade

Deci, trebuie să înțelegeți „legea“, care este la locul de muncă aici:

1. Se determină semnul funcției în trimestrul corespunzător.

2. Notă următoarele:

modificări funcționale pentru a kofunktsiyu

Funcția pe kofunktsiyu neschimbată

Ceea ce se înțelege prin - modificări ale funcției la kofunktsiyu?

Răspuns: sinus și cosinus modificări sau invers, tangenta la cotangentă, sau vice-versa.

Acum, reprezentat de lege, vom scrie câteva formule de reducere pe cont propriu:

Acest unghi se află în al treilea trimestru, în al treilea trimestru cosinusul este negativ. Funcția pe kofunktsiyu nu se schimba, pentru că avem 180 de grade, aceasta înseamnă:

Unghiul se află în al treilea trimestru, în al treilea trimestru cosinusul este negativ. Schimbarea funcției pe kofunktsiyu, pentru că avem 270 de grade, aceasta înseamnă:

Unghiul se află în primul cadran, sinusul este pozitiv în primul cadran. Noi nu se schimba caracteristica pe kofunktsiyu, pentru că avem 360 de grade, deci:

Acolo aveți o confirmare suplimentară că sinusurile unghiuri adiacente sunt egale:

Unghiul se află în al doilea cvadrantul, al doilea trimestru sinusul este pozitiv. Nu modificați caracteristica pe kofunktsiyu, pentru că avem 180 de grade, aceasta înseamnă:

Lucrul prin mental sau în scris, fiecare formulă și veți vedea că nimic complicat.

În articolul privind soluția unui triunghi dreptunghic a fost marcată de acest fapt - sinusul unui unghi ascuțit într-un triunghi dreptunghic este egal cu cosinusul celuilalt unghi ascuțit în ea.

Și invers - cosinusul unghiului ascuțit într-un triunghi dreptunghic este egală cu sinusul unghiului ascuțit al celuilalt în ea. Aici aveți o confirmare a acestei formule de o reducere:

Desigur, pentru a determina valorile unghiurilor este posibilă fără a aduce formule de cerc trigonometrice. Și dacă o poți face foarte bine. Dar pentru a înțelege modul în formulele de reducere, o poti face foarte repede.

Aceste formule pot fi exprimate sub formă de tabel:

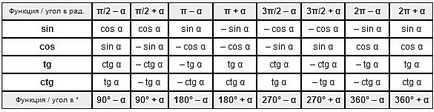
Atunci când în sarcina vor folosi formule de reducere, asigurați-vă că se va referi la acest articol, astfel încât să fie întotdeauna în măsură să perie pe teoria prezentată mai sus. Asta e tot. Sper că materialul a fost de folos.

Obțineți materiale articol în format PDF

Cu stimă, Aleksandr Krutitskih.