Metode pentru graficul task
În matematică, mult mai puternic decât în alte discipline găsite trăsătură de organizare, străduindu-se pentru a găsi ordinea ascunsă în tot ceea ce ne înconjoară.
Există diferite modalități de specificare a graficului: geometrice (desene, scheme, diagrame), o simplă listă de noduri și muchii, tabelare. Omul este convenabil de a lucra cu numărul de-model, deoarece se poate stabili cu ușurință conexiune între nodurile în formă vizuală folosind nervuri descrise cu linii continue. O astfel de reprezentare geometrică a unui grafic planar se numește punerea sa în aplicare. Prelucrare mai ușor de a seta numărul în formă algebrică - enumerare (listă) nodurile sau margini.
De exemplu, un grafic direcționat în Fig. 2.3 poate fi definită prin perechi (V1, V2), (V2, V3), (V2, V3) și (V1, V1), care corespunde arce (r și, t, s). Pe parcursul tranziției de la o metodă geometrică algebric la același grafic poate corespunde cu diferite imagini grafice - izomorfe, imaginile corespunzătoare depinde, de exemplu, proprietatea realizability plat. Pentru a face acest lucru, trebuie să setați în mod corespunzător însuși COUNT.
Principala cale de a specifica numărul este de a lista toate nodurile și marginile sale. Dar o astfel de vedere, în primul rând, asimetrici (cu el dificil de a lucra cu, mai ales calculatoare), și în al doilea rând, pentru a specifica fiecare margine aveți nevoie de mai mult timp pentru a scrie nodurile corespunzătoare care rău în termeni de compresie și de stocare. Uneori, graficul dat tabel care constă din n rânduri (sus) și m coloane (coaste). În principal, toate metodele de grafic sarcină (un tabel matrice grafic) este de a specifica corespondența dintre seturile de n noduri Vi și t marginile X i.
Una dintre cele mai comune modalități de a specifica grafic este metoda matricei. Să presupunem că avem un grafic G (V, X), unde V = 1, V2. Vn> - blaturi și X = 1, X2 ,. Xm> - marginile graficului.
Noi numim masa de matrice de incidență B, formată din n rânduri (sus) și m coloane (coaste), în care:
pentru un graf neorientat:
pentru un grafic direcționat:
Evident, în fiecare coloană a matricei de incidență trebuie să fie doar două nenulă număr, deoarece marginea este incident două vârfuri. Numărul de elemente nenule în fiecare rând - gradul de vertexul corespunzător. Dar, în matematică mai ușor de a lucra cu matrice pătrate, ca instrumente algebrice adecvate sunt bine concepute pentru ei.
Noi numim matricea de adiacență a grafului G (V, X) fără margini multiple O matrice pătrată de ordinul n, în care:
Deoarece pentru o muchii grafuri neorientate (Vi. Vj) și (Vj. Vi) simultan aparțin sau nu aparțin graficului, așa cum simbolizează una și aceeași margine, Aij == aji. Matricea de adiacență a unui graf neorientat este simetrică și nu se schimbă atunci când transpune.
Deși formal fiecare nod întotdeauna adiacent în sine, în matricea de adiacenta am pus aij = 0 dacă nu are bucle și aij = 1 dacă există o buclă. Deci, în cazul în care graficul este matricea de adiacenta și nu depinde de diagonala principală întotdeauna zerouri.
De exemplu, un grafic direcționat în Fig. 2.3 Puteți seta o incidență tabel (tabelul 2.1.).
Tabelul 2.1. Tabelul digraph incidență
Un grafic cu margini multiple (grafic special direcționat), este dificil de stabilit folosind matricea adiacenta. Să o facem în mod oficial. Dacă graficul este neorientat, atunci avem AIJ Aji ==. și este egală cu multiplicitatea nervurilor (Vi. Vj). În special, dacă i = j, atunci aij - numărul de bucle în Vi. Dezavantajul acestei abordări constă în faptul că rămâne necontabilizate pentru amenajarea reciprocă a mai multor margini. Astfel, nervurile se pot suprapune reciproc, care, din păcate, nu afectează matricea de adiacenta.
Rețineți că pentru această determinare un grafic direcționat fără margini paralele ale graficului este un caz particular al graficului cu mai multe nervuri la fiecare multiplicitate muchie egală cu 1 sau 0. Este evident că pentru două vârfuri Vi și Vj (i¹j) există două posibilități de bază:
Dacă toate marginile merg de la unul la altul și include partea de sus
sau în cazul în care pentru fiecare nod există ambele margini de intrare și de ieșire.
Lăsați multitudinea completă a muchiilor egală cu n. în timp ce de la vertex la nodul Vj Vi emane m £ n margini, și a Vj Vi provin din n - m coaste. Apoi AIJ celula de scriere m. și Aji celule scrie n - m Dacă există mai multe bucle, ele sunt toate conectate cu un singur vârf Vi .. Prin urmare, în aii de celule de scriere multiplicitatea bucle la Vi.
Un astfel de grafic sarcină are aceleași dezavantaje ca și orientat, și totuși neglijare direcția aranjament reciproc. Cu toate acestea, principalul dezavantaj este că, cu această definiție a matricei de adiacenta (ca un grafic cu mai multe margini, și fără ele) nu este întotdeauna posibil să se determine printr-o matrice de adiacență grafic direcționat sau nu.
Incidența matriciaz nici o astfel de problemă, deoarece prezența elementului de formular este -1 graf orientat criteriu. Pentru adiacenta asimetrie matrice poate fi suficientă pentru orientare, dar nu și un criteriu. De exemplu, un grafic cu matrice adiacenta poate corespunde segmentului V1 V2 (și două vârfuri) - sau un grafic neorientat inel cu două muchii V = 1, V2); (V2, V1)> - digraph. Acesta dezavantaj -essential, și el a apărut doar atunci când încearcă să determine matricea de adiacenta pentru un grafic cu mai multe muchii este, prin urmare, pentru a specifica un grafic direcționat cu matrice de adiacență (în cazul în care se dovedește simetrică) trebuie să specifice fie acest lucru separat, de exemplu de AOP sau orice element al scrie matrice "-".
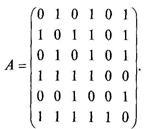
Problema 19. Să presupunem că graficul G este dată matricea de adiacenta A. Diagramele din acest grafic, dacă
Problema 20. Să presupunem că graficul G este dată matricea de adiacenta A. Diagramele din acest grafic, dacă
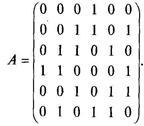
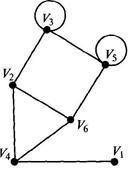
Decizie. Grafic grafic cu șase vârfuri, reprezentăm în Fig. 2.19.
Orice grafic direcționat este o relație binară A V, în care o multitudine de vârfuri de V, X și perechi de coaste.
Pentru un număr finit de vârfuri V raportul X poate fi reprezentat în trei moduri:
grafic, adică Diagrama (Figura 2.19.);
prin utilizarea de tabele care sunt reprezentate de 1 și 0;
utilizând matrici (în cazul matricelor adiacenta).
Această formă a relației este utilă în rezolvarea multor probleme logice și industriale. Este, de asemenea, utilizat în prelucrarea pentru a organiza informațiile