Piramida în care diedrului unghiurile baze egale

Acum, ia în considerare piramida, în care unghiurile diedre de la baza sunt egale cu ceea ce sunt reprezentate proprietățile lor.

Dacă toate unghiurile diedre la marginile bazei sunt egale.

1) vârful piramidei este proiectată în centrul cercului inscris la bază;

2) Baza piramidei este proiecția ortogonală a suprafeței sale laterale. cu toate acestea zona baza piramidei pot fi găsite prin formula

- unghiul diedru la baza piramidei. În cele mai multe cazuri, această formulă este folosită pentru a găsi zona suprafeței laterale a piramidei:

Prin urmare, suprafața totală a piramidei este

3) suprafață laterală, în acest caz, poate fi găsită prin formula

unde p - bază semiperimetrul, l - înălțimea marginii laterale trase din vârful piramidei.

Triunghiurile dreptunghiulare formate prin înălțimea piramidei, înălțimile fețele laterale trase din vârful piramidei și proiecțiile lor (egală cu raza cercului inscris) sunt egale. Prin urmare, de asemenea,

- înălțimea fețelor laterale desprinse din vârful piramidei, sunt egale;

- înălțimea fețelor laterale care formează o piramidă cu o înălțime de unghiuri egale.

Rezolvarea problemelor într-o piramidă în care unghiurile diedre de la baza egală (sau - piramidă, în care înălțimea fețelor laterale sunt fie formate cu o înălțime unghiuri egale piramidă), începe cu desen.

În cazul în care baza piramidei - triunghi

Centrul cercului înscris în triunghiul se află strict în triunghiul și un punct de intersecție a Bisectors ea.

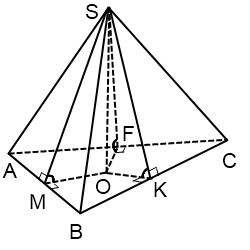
Raza cercului caută formula inscripționată

unde S - aria triunghiului, p - perimetrul său de podea.

În cazul în care baza piramidei este un triunghi dreptunghic. desen un pic diferit.

Acest lucru se datorează proprietăților ingineriei concurente: paralelism directă este menținută. Razele perpendiculare cateta, și segmentele adiacente unghiului drept al triunghiului, o formă pătrată, care este reprezentat în desen paralelogramului.

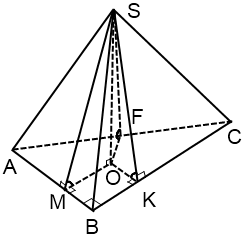
Raza cercului înscris în triunghi dreptunghiular formula căutarea

unde a și b - picioarelor, c - ipotenuzei.

În cazul în care baza piramidei - un paralelogram

Dintre toate paralelograme un cerc este înscriem posibilă numai în diamant (și un pătrat ca un caz special). Prin urmare, dacă o problemă este cunoscut faptul că toate unghiurile diedre bază egală (sau înălțimea fețelor laterale ale piramidelor sunt formate fie de o înălțime a piramidei unghiuri egale), iar baza este un paralelogram, atunci putem vorbi doar de diamant (sau pătrat).

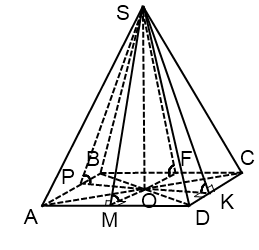
O - punctul de intersecție al diagonalelor unui romb (pătrat).

Raza cercului inscris in diamant pot fi găsite în conformitate cu formula

Mai mult decât atât, raza cercului înscris în rombul este jumătate din înălțimea sa.

În cazul în care baza piramidei - un patrulater arbitrar

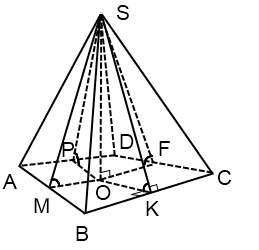
Despre - punctul de intersecție al Bisectoarele ABCD patrulater.

Raza cercului înscris în patrulaterul caută aceeași formulă

Așa cum înscrisă în cercul patrulater poate fi dacă și numai dacă suma lungimilor laturilor opuse sunt egale,

În cazul în care baza piramidei - Keystone

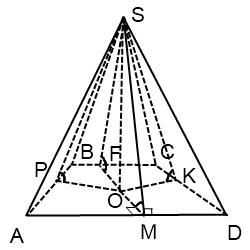
O - punctul de intersecție al Bisectoarele trapezul.

Raza cercului înscris în trapezoid

și raza cercului înscris este egal cu jumătate din înălțimea trapezului.

Dacă toate unghiurile diedre de la baza piramidei sunt egale (sau înălțimea fețelor laterale ale piramidei sunt egale, sau înălțimea fețelor laterale ale piramidei fac unghiuri egale), iar în partea de jos a piramidei - un poligon regulat, este - piramida regulată.