Scădeți suma numerelor - claselor inițiale, lecții

- Suficient pentru ca toată lumea să facă o dorință. Dar avem o lecție de matematică, prin urmare, începe să numere.

- Ce grupuri pot partaja toate numerele?

- Din ce motive? (Neambiguă, două cifre)

- Care sunt numerele în ordine crescătoare. (4, 15, 27, 53, 75, 96.)

- Găsiți diferența dintre cele mai vechi și cel mai tânăr stele. (92.)

- Oferă informații despre numărul 92. (Acesta este un număr format din două cifre în ea 9 zeci, 2

unitate, vecinii săi 91 și 93, suma numerelor 11.)

- Scriem numărul 92 este frumos și corectați întreaga linie.

b) Dar două stele mari strălucesc.

- Care sunt semnale? Ce spun ei? (Expression).

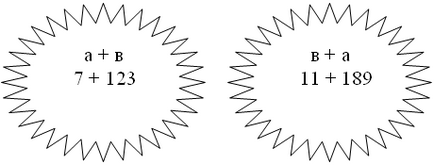
- Care sunt expresii? (Numeric și alfabetic).

- Citește scrisoarea de exprimare. (A + b, + a).

- Ce ne spun? (Arată Comutativitate de adăugare.)

- Citește expresia numerică. (7 + 23, 11 + 89)

- Se calculează valoarea lor prin aplicarea Comutativitate de adăugare.

- Ceea ce schimb termeni? (Pentru comoditatea calculelor.)

c) Astronauții a plecat în zbor. Până la destinația finală au zburat 2 săptămâni și 14 zile înapoi. Cum se explica aceasta diferenta? (2 săptămâni = 14 zile).

d) Acum vom rezolva problema în diferite moduri (la partea din spate a plăcii):

Kid și Carlson trebuie să atragă în cerul de noapte de stele 86. Kid a atras 36 de stele, și Carlson 45. Câte asteriscuri au părăsit egalitatea pe cerul înstelat?

- Ce această sarcină?

- Ce știm? Ce este? (Integer).

- Ce altceva mai știm? Ce este? (piese).

- Care sistem este potrivit pentru această sarcină? (Prima).

- De ce? (Este necesar să se găsească o parte.)

- Cum știi cât de mult este lăsat să atragă stele? (86 - 36 - 45.)

- Cât de diferit? (86 - (36 + 45)).

- Comparați expresie. Ceea ce au în comun? (numere identice.)

- Care este diferența? (În prima parte a primei scade 1, și apoi celălalt;

în al doilea rând scăzând suma numerelor numerelor 36 și 45.)

- Găsiți valoarea fiecare expresie. (5)

- Cât de multe stele la stânga pentru a desena Kid și Carlson? (5)

3. Declarația scopului lecției.

- Oh, ce e asta? Cineva a aruncat o altă stea (pe masa):

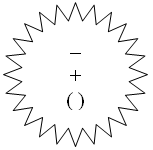
- Cineva astăzi face minuni.

- Ceea ce este scris pe stea? (Marks și paranteze.)

- De ce le-am plantat?

- Ce știi despre semnul minus? (Utilizarea prin scădere.)

- Ce sunt acolade? Cum programul în cazul în paranteze se schimbă?

(Schimbarea ordinii acțiunilor.)

Guess: probabil, aceste semne ne vor ajuta în sala de clasă.

- Se înregistrează următoarea expresie: 87 - (15 + 7).

- Cum convenabil pentru a scădea 87 din numărul de suma numerelor 7 și 15?

- Din vychest7 87 mai întâi, și apoi un alt 15. transformă 65.

- Am schimbat cursul acțiunii. Am terminat?

- Să examinăm această expresie prin înlocuirea numărului de litere: a - (b + c) și -sa - a.

- Problemă: Sunt egali? (Elevii dau răspunsuri diferite.)

- Cine formulează obiectivul lecției noastre?

(Se determină dacă vyrazheniyaa egal cu - (a + c) și a - a - a).

- De ce avem nevoie de asta? (Pentru a afla cum să rațional: rapid și ușor pentru a efectua calcule.)

- Efectuați numărul de activitate 1 - Exemplul 1, 2p. - 2 exemplu, 3p. - 3 exemplu.

Cu fiecare rând merge un elev.

Elevii scrie într-o expresie de notebook-uri:

- Comparați expresie. Ce place? Care este diferența?

- Cum convenabil să-și asume? (Preferat dintre cantitatea scade.)

83 - (19 + 31) = 83-50 = 33.

Spațiu discotecă, copii efectua miscari de dans.

Soluția problemei №3 p.50

În prima lună - 45 kg ←

În a doua lună -. 5 kg pentru bărbați.

45-5 = 40 (kg) - ziua a 2-a mâncat

50-45 = 5 (kg) - stânga

8. Munca creativă.

Gruparea. Fiecare elev pe figura geometrică de birou: un triunghi, un pătrat sau dreptunghi.

- Amintiți-vă că acest perimetru. (Suma lungimilor tuturor părților.)

- Cred că vorbesc despre niște cifre:

Pentru a calcula perimetrul figurii doar o singură măsurătoare. (Pătrat).

Pentru a calcula perimetrul această cifră este suficient să se știe 2 măsurători. (Dreptunghi).

Pentru a calcula perimetrul această cifră este suficient să se știe 3 măsurători. (Triangle).

- Și, în orice caz, este suficient să se știe o parte a triunghiului? (Când este echilateral.)

- 1 este o serie de perimetru al triunghiului într-o singură dimensiune - 5 cm.

- Numărul 2 este egală cu pătratul perimetrului cu aceleași dimensiuni laterale - 5 cm.

- 3 este o serie de perimetru dreptunghiular având două dimensiuni - 5 cm și 1 cm.

- Ce regulă am învățat în clasa de astăzi?

- Pe măsură ce se poate deduce suma de numere?

- Acum, închide ochii. Faceti o dorință și puneți-l pe palma birou. Imaginați-vă că priviți cerul cosmic.

Profesor include muzică spațiu.

- Dacă acum palma stea cade, dorința va deveni realitate.

Fiecare elev primește un asterisc.

10. Tema

11. Evaluarea cunoștințelor copiilor.

- Vă mulțumesc pentru lecție.