site-ul personal - funcția extremelor

funcţia extremelor

Extremum numita funcție minimă valoare maximă sau pe un set dat.

punctul extremum - punctul în care valoarea maximă sau minimă funcție.

Punctul maxim - este atins un punct în care valoarea maximă a funcției.

punctul minim - punctul în care funcția atinge o valoare minimă.

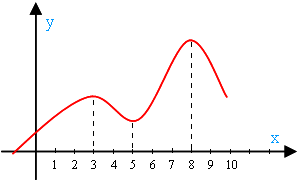
Cifra din vecinătatea x = 3, funcția atinge o valoare maximă (adică, în vecinătatea acestui punct nu este punctul de mai sus). În imediata apropiere a x = 8 din nou, are o valoare maximă (din nou clar: este în acest cartier nici un punct de mai sus). La aceste puncte, creșterea scădere a înlocuit. Acestea sunt punctele de maxim:

In vecinatatea lui x = 5 este atins valoarea minimă a funcției (adică, în vecinătatea x = 5 puncte sub nr). În acest moment, reducerea se înlocuiește cu o creștere. Este un minim:

Punctul maxim și minim de puncte sunt funcții extreme. și valorile funcției de la aceste puncte - extremele ei.

punctul Ho este un punct de maxim. dacă are un cartier la toate punctele unde f (x) este mai mică sau egală cu f (Ho):

formulare simplificată. dacă la Ho modificări derivate semn de la plus la minus, atunci Ho este punctul maxim.

ho este un minim punct. dacă are un cartier la toate punctele unde f (x) este mai mare sau egal cu f (Ho):

formulare simplificată. în cazul în care la modificări derivate Ho semn de la minus la plus, atunci Ho este un punct minim.

Puncte critice și staționare ale funcției:

Punct interior de definire a funcției în care funcția este continuă, dar derivatul nu există, numit un punct critic.

Domeniul punctului intern al funcției pentru care derivatul este zero, numit punctele fixe.

O condiție necesară pentru o extremum:

Dacă Ho - punctul extremum de f (x), apoi la acest punct sau se anulează derivate (acest punct staționar) sau derivat nu există (punctul critic).

condiția suficientă a extremelor:

Să Ho - un punct critic. În cazul în care derivatul f „(x) la trecerea de la stânga la dreapta prin punctul Ho schimbă semnul de la plus la minus, Ho - un punct maxim:

În cazul în care derivatul f „(x) la trecerea de la stânga la dreapta prin punctul Ho schimbă semnul de la minus la plus, Ho - punctul minim:

Dacă trec prin punctul critic al derivatului nu se schimbă semnul, apoi la punctul Ho nu este extremelor.

Pe intervalul [a, b] funcția y = f (x) poate ajunge la cea mai mică sau cea mai mare valoare sau punctele critice sau segmentele de la capete [a, b].

2) Găsiți fix (f '(x) = 0), și critic (f' (x) nu există) ale funcției punctului y = f (x).

3) Marcați punctele staționare și critice pe linia de numărul și determină semnul derivatului pe golurile rezultate.

4) Pentru a trage concluzii cu privire la monotonia funcției și punctele sale de extremelor.