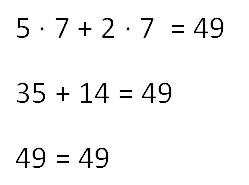Soluția de complex de ecuatii de grad 5
Sub un complex ecuații (compozit), înțelegem ecuațiile, care conțin două sau mai multe operații aritmetice.
Soluția acestor ecuații se realizează prin aceleași reguli pe care le-am uitat la pagina, „Soluția este ecuații simple de gradul 5„în același subiect.
Dar soluția ecuațiilor de compozit este produs într-o anumită secvență.
- Noi aranja procedurile din ecuație.
- Stabilim necunoscut pe ultima acțiune. Ultima acțiune în această ecuație - această deducere. Vă rugăm să rețineți că, în acest stadiu al necunoscut nostru - este «5ani», și că este ceea ce noi considerăm a fi reduse.
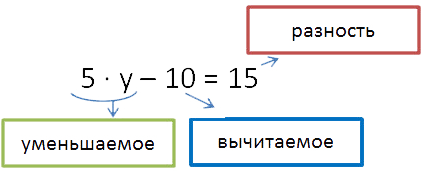
- Noi decidem ca o ecuație simplă și pentru a găsi «5Y». Să ne amintim regula pentru identificarea necunoscut este redusă.
Pentru a găsi necunoscut este redus, este necesar să se adauge diferența se scade.
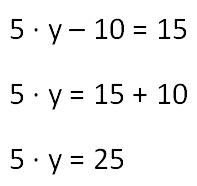
Pentru a găsi factorul necunoscut, produsul ar trebui să fie împărțit într-un factor de bine-cunoscut.
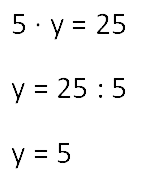
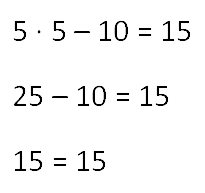
Așa e. Deci, ecuația este rezolvată corect.
Un alt mod de a rezolva ecuații complexe
Unele (ecuația compozite) complexă poate fi rezolvată într-un alt mod. Cunoașterea proprietăților și fiind capabil să aplice adunarea și scăderea precum și înmulțire și împărțire proprietăților, ecuațiile sunt rezolvate după cum urmează.
(X + 54) - 28 = 38
- Noi simplifica expresia de pe partea stângă a ecuației, folosind una dintre proprietățile de scădere.
Pentru a ține departe de cantitatea de numere care aveți nevoie pentru a scădea acest număr de la un termen și se adaugă rezultatul scăderii cu alți termeni.
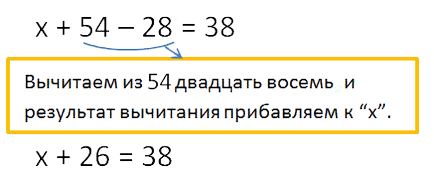
(12 + 54) - 28 = 38
66-28 = 38
Simplificarea expresiilor în ecuațiile
Dacă ecuația este întâlnită expresii care pot fi simplificate, prima simplifica expresia, și numai apoi rezolva ecuația.
Partea stângă a ecuației poate fi simplificată. Hai să o facem.
Acum vom rezolva ecuație simplă, de regula de a găsi un factor necunoscut.
După finalizarea exemplu, efectuați verificările.