Soluția problemelor în fizică - potențialul câmpului electrostatic

Soluția problemelor în fizică - potențialul câmpului electrostatic

Înainte de a începe să abordeze problemele tipice, amintiți-vă informațiile teoretice de bază legate de acest subiect:

• Câmpul electrostatic este potențial. Acest lucru înseamnă că activitatea forțelor de câmp electric atunci când se deplasează în sarcina fiecărui traseu închis este zero. În cazul în care calea de deplasare a taxei nu este închisă,

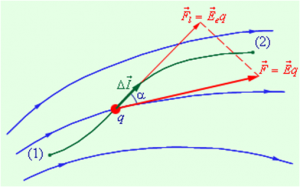
Lucrul energiei electrice pentru o deplasare mică a taxei

funcționarea câmpului electrostatic în acest caz este definită după cum urmează: AA = Ec Δl cos α, în care E - intensitatea câmpului la un anumit punct, q - cantitatea de încărcare, Δl - amplitudinea deplasării mică a încărcăturii, α - unghiul dintre direcția intensității câmpului și deplasarea de încărcare.

• Dacă mutați sarcină q din punct de potentialul energetic W1 în punctul cu potențial energetic W2. diferența dintre aceste energii va fi egal cu lucrul mecanic. care fac câmpul electric la aceasta: A = W2 - W1.

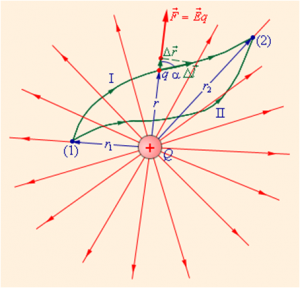
Lucrul mecanic efectuat de câmpul în timp ce se deplasează taxa de la un punct la altul, este egală cu diferența în energiile potențiale de încărcare la aceste puncte

• Potențialul câmpului electric - cantitatea scalară fizică, egală cu raportul dintre energia potențială a sarcinii electrice la un moment dat câmpului electrostatic la amploarea acestei taxe:

Caracteristica energetică a câmpului - potențial. În sistemul internațional de unități (SI) unitatea de capacitate este volt (V).

• Potențialul domeniul punctului de evacuare și sfera încărcată definită de relația:

unde r - distanța de centrul sferei sau o taxă la un anumit punct în spațiu (în cazul unei sfere, acest punct ar trebui să fie plasat în afara sferei), q - valoarea de încărcare, k = 9 × 10 9 N · m 2 / C 2 - coeficient constant. Potențialul în interiorul sferei în orice punct este aceeași și egală cu potențialul pe suprafața sa:

unde R - raza sferei.

• Lucrările la mișcarea zaryadaq electrice dintr-un punct în spațiu în altul este produsul taxei pe diferența de potențial dintre aceste puncte: A12 = q (φ2 - φ1).
• Tensiunea între două puncte de câmp electrostatic uniform și intensitatea acestui domeniu sunt legate de: U = Ed. în cazul în care d - distanța dintre suprafețele echipotențiale, care aparțin acestor puncte.

Ne întoarcem acum la rezolvarea problemelor. Ca întotdeauna, eu recomand cititorului să decidă propria lor în primul rând, iar soluția rezultată se compară cu cele prezentate in articol. Unele sarcini sunt preluate din opțiunile reale de examen în Fizică de la diferiți ani, precum și ajutoare recomandat să se pregătească pentru acest examen.

Problema 1. Atunci când se deplasează între punctele de încărcare cu o diferență de potențial de 1 kV câmp electric de lucru dedicat 40 mJ. Care este tariful?

Problema 2. Într-un câmp electric uniform de 60 kV / m este 5 taxa nC mutat. Mutarea modulo egale de 20 cm, 60 formează un unghi 0 cu direcția liniei de alimentare. Găsiți câmp de funcționare, modificarea potențialului energetic al câmpului de încărcare și interacțiunile și tensiunea între punctele de început și sfârșit de deplasare. Oferiți răspunsuri la aceleași întrebări în cazul mișcării o sarcină negativă.

Soluție: Munca de teren pe mișcarea de încărcare poate fi calculată în conformitate cu formula A = EQL cos α = 60 · 10 3 · 5 x 10-9 · 0,2 · cos 60 0 = 3 x 10 - 5 J Schimbarea energie potențială în acest caz este un loc de muncă perfectă. De aceea: ΔW = -A = - 3 × 10 - 5 J (energia potențială a scăzut). Tensiunea este determinată de intensitatea câmpului conform formulei: U = Ed = El cos a, ca în acest caz, taxa transferată la un unghi față de direcția liniilor de forță. Astfel, U = 60 x 10 3 · 0,2 · cos 60 = 0 6000 V. În cazul unei valori de sarcină negativă A și ΔW schimba pur și simplu semn.

A: 3 x 10 - 5 J - 3 x 10 - 5 J, 6000, · 10 -3 - 5 J 3 x 10 - 5 J, 6000 V.

Problema 3. electronic mutat în câmpul electric de accelerare cu un potențial de la punctul B la punctul 200, cu un potențial de 300 V. Găsiți energia cinetică a electronului, o schimbare în energia sa potențială și viteza dobândită. Viteza de electroni inițial să fie zero.

Soluție: lucru, care a făcut câmp în timp ce se deplasează de electroni găsi după cum urmează: A12 = q (φ2 - φ1) = 1,6 · 10 -19 · (300 - 200) = 1,6 x 10 -17 J. Prin urmare schimbați în energia potențială a unui electron în domeniu. egal cu :. ΔW = -A = - 1,6 · 10-17 J. Această scădere este compensată prin creșterea energia cinetică la aceeași valoare, astfel cum rezultă din conservarea energiei: E = 1,6 · 10-17 G. Deoarece E = m υ 2 /. 2, apoi υ = √ (2E / m) = √ (2 x 1,6 x 10-17 x 10 /9.1 - 31) = 6 mm / s.

Răspuns: 1,6 x 10 - 5 J - 1,6 x 10 - 5 J 6 mm / s.

Problema 4. Ce diferență de potențial trebuie să treacă un electron la viteza a crescut de la 10 la 30 mm / s?

Soluție: Modificarea energiei cinetice a electronilor atunci când trece o astfel de diferență de potențial poate fi găsit din relația: AE = m υ2 2/2 - m υ1 2/2 = 8/18 · 9.1 · 10-31 · (30 · 10 6) 2 = 3,6 · . 10-16 G. aceeaşi modificare în conformitate cu legea de conservare a energiei egală cu munca pe care a comis, în acest caz, câmpul electric :. E = -A = -3.6 · 10-16 J Utilizarea raportului înregistrat la început, obținem: φ2 - φ1 = a / q = -3.6 · 10 - 16 / 1,6 x 10 -19 = -2,250 V.