Soluția sistemului de ecuații liniare

Sistemul de ecuații liniare

Sistemul ecuație este scris de obicei într-o coloană de unul deasupra celuilalt și sunt combinate cu bretele

Sistemul de ecuații de forma în care a, b, c - numărul și x, y - variabile, se numește un sistem de ecuații liniare.

În rezolvarea sistemului de ecuații folosind proprietățile, doar pentru a rezolva ecuațiile.

Solutia de sistem liniar ecua metoda substituției

1) exprimă variabilă într-una din ecuațiile. De exemplu, putem exprima y în prima ecuație, obținem sistemul:

2) Membru supleant în a doua ecuație în loc de 3-y expresie 7:

3) Rezolva a doua ecuație obținută:

4) Soluția obținută este substituită în prima ecuație a sistemului:

Sistemul de ecuații are o soluție unică: o pereche de numere x = 1, y = -4. Răspuns: (1; 4). Este scris în paranteze, prima valoare pozitia x. al doilea - y.

Soluția sistemului de ecuații liniare metodei de adăugare

Noi rezolva sistemul de ecuații din exemplul precedent prin metoda de adăugare.

1) Conversia sistemului, astfel încât coeficienții de una dintre variabilele devin opuse. Inmultiti prima ecuație a sistemului de „3“.

2) Ori termwise ecuația sistemului. A doua ecuație a sistemului (orice) rescrie neschimbat.

3) Soluția obținută este substituită în prima ecuație a sistemului:

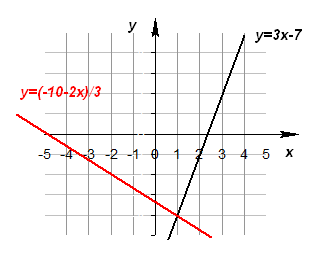
Soluția sistemului de ecuații liniare grafic

Grafice rezolvarea ecuații simultane cu două variabile se reduce la punctele de coordonate în ecuații grafice comune Preluarea.

Graficul unei funcții liniare este o linie dreaptă. Două linii în plan se pot intersecta la un moment dat, să fie paralele sau coincid. Prin urmare, sistemul de ecuații poate: a) să aibă o soluție unică; b) nu are soluții; c) să aibă un număr infinit de soluții.

2) Sistemul de ecuații este punctul (dacă ecuațiile sunt liniare) graficele de intersecție.

Soluție grafică a sistemului

Metoda de introducere a noilor variabile

Variabilele de substituție poate conduce la soluția unui sistem de ecuații simplu decât originalul.

Luați în considerare soluția sistemului

Introducem un înlocuitor, atunci

Ne întoarcem la variabilele originale

cazuri speciale

Fără rezolvarea unui sistem de ecuații liniare, putem determina numărul deciziilor sale privind coeficienții variabilelor corespunzătoare.

Având în vedere un sistem

1) În cazul în care sistemul are o soluție unică.

2) În cazul în care sistemul nu are soluții. În acest caz, directă, este graficul sistemului de ecuații sunt paralele și nu coincid.

3) În cazul în care sistemul are un număr infinit de soluții. În acest caz, liniile coincid unele cu altele.

Metoda de eliminare secvențială a necunoscutelor, rezultând într-un sistem de ecuații liniare în formă eșalon.