variabile aleatoare
variabile aleatoare discrete și continue
Unul dintre conceptele de bază ale teoriei probabilității este conceptul unei variabile aleatoare. O valoare aleatoare este valoarea care este un rezultat al testului de o multitudine de valori posibile ale acestora numai are una, de altfel, nu se știe care unul.
Variabile aleatoare sunt discrete si continue. Discrete valoare aleatoare (DSV) este variabila aleatoare care poate lua un număr finit de izolat reciproc valori, adică În cazul în care pot fi numărate valori posibile ale acestei magnitudine. Continuă valoare aleatorie (NSV) este o variabilă aleatoare, toate valorile posibile care umplu complet un anumit interval de număr de linie.
Valorile aleatorii sunt indicate în litere latine de capital X, Y, Z, etc. Valorile posibile ale variabilelor aleatoare sunt notate cu litere mici corespunzătoare.
Înregistrarea înseamnă „probabilitatea ca o variabilă aleatoare are o valoare de 5 este egal cu 0,28.“
Exemplul 1. Odată ce a aruncat zarurile. În acest caz, poate cădea un număr de la 1 la 6, indicând numărul de puncte. Denote aleatoare X = variabila. Această valoare aleatoare, ca rezultat al testului poate lua numai una dintre cele șase valori: 1, 2, 3, 4, 5 sau 6. În consecință, variabila aleatoare X este DCB.
Exemplul 2. Când a aruncat o piatră el zboară o oarecare distanță. Denote aleatoare X = variabila. Această variabilă aleatoare poate lua orice, dar numai una, valoarea unei anumite perioade. În consecință, variabila aleatoare X este MPR.
Acționează de distribuție variabilă aleatoare discretă
O variabilă aleatoare discretă se caracterizează prin valori pe care le poate lua, și probabilitățile cu care sunt luate aceste valori. Corespondența între valorile posibile ale variabilei aleatoare discrete și probabilitățile corespunzătoare se numește legea distribuției variabile aleatoare discrete.
În cazul în care toate valorile posibile
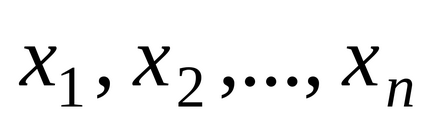
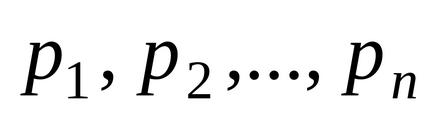
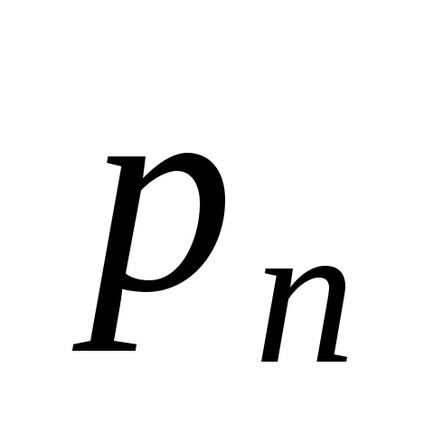
lege de distribuție DSV pot fi reprezentate grafic, în cazul în care sistemul să reprezinte punctul de coordonate rectangular
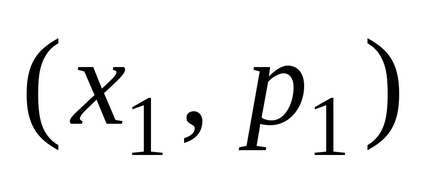
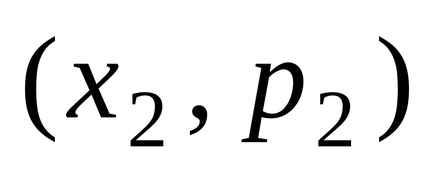
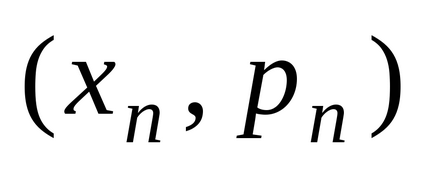
și să le conecteze pe segmente de linii drepte. Cifra rezultată se numește o distribuție poligon.
Exemplul 3. Cerealele trebuie curățat, conține 10% din buruieni. 4 boabe selectate în mod aleatoriu. Denote aleatoare X = variabila. Construiește o lege de distribuție DSV X și distribuție poligon.
Decizie. De exemplu, starea. apoi:
;
;
;
;
.
Scriem legea de distribuire a X DSV sub forma unui tabel și a construi o distribuție a unui poligon:
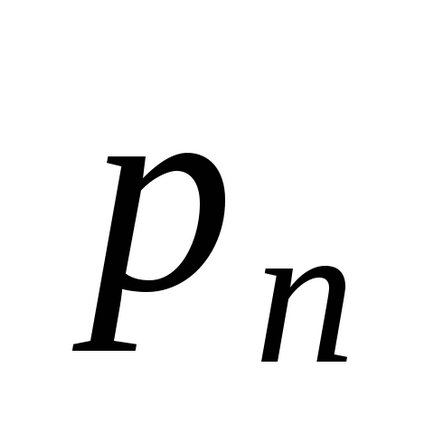
Așteptarea X este DSV suma fiecare valoare a acestei cantități pe probabilitatea corespunzătoare :.
Așteptarea unei variabile aleatoare este aproximativ egală cu media aritmetică a valorilor sale. Prin urmare, în probleme practice iau de multe ori speranța de valoarea medie a acestei variabile aleatoare.
Primer8. Shooter emboss 4, 8, 9 și 10 puncte pentru probabilitățile de 0,1, 0,45, 0,3 și 0,15. Găsiți numărul estimat de puncte într-o singură lovitură.
Decizie. Denote aleatoare X = variabila. Apoi. Astfel, numărul mediu așteptat de la un împroșcat puncte împușcat este egal cu 8,2, iar în 10 imagini - 82.
Principalele proprietăți ale așteptările sunt:

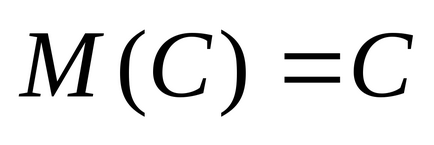



diferență
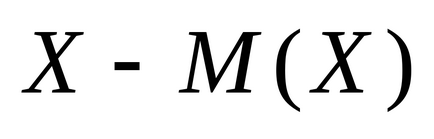
Dispersia variabilei aleatoare discrete
Pentru a caracteriza variabila aleatoare, cu excepția speranța matematică și este utilizată variația. ceea ce face posibilă evaluarea valorilor dispersiei (variație) a variabilei aleatoare în jurul așteptărilor sale. La compararea a două variabile aleatoare uniforme cu așteptările matematice egale „cel mai bun“ valoare este cea care are intervalul mai mic, adică variație mai mică.
Varianța variabila aleatoare X este speranța matematică a pătratul abaterii unei variabile aleatoare de la așteptările sale matematice :.
În probleme practice pentru calcularea varianței cu ajutorul formulei echivalente.
Principalele proprietăți ale dispersiei sunt:

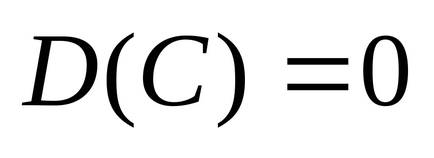


Dispersia caracterizează dispersia variabilei aleatoare în jurul medie și așa cum se vede din formula, măsurată în unități pătrate în comparație cu unitățile variabilei aleatoare. Prin urmare, deviației standard pentru unitățile introduse Armonizare răspândirea variabilă aleatoare de măsurare cu valoarea unităților de măsură
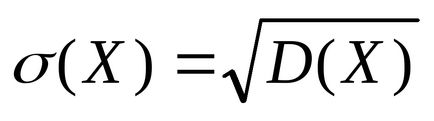
Primer9. Găsiți varianța și deviația standard a dreptului de distribuție DSV H. predeterminată: