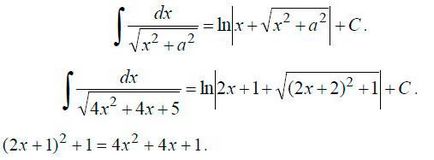11 O soluție de integralele

soluție integrală. Spune cum să rezolve integralele.

Integral - conceptul matematic avansat al sumei. Integrale soluție sau prezența lor se numește integrare. Utilizarea integrală posibil pentru a găsi valori, cum ar fi zona, volum, greutate și mai mult. Decizia integralelor (integrare) este operația inversă diferentsiirovaniyu. Pentru a obține o idee mai bună a ceea ce este integrala, vom reprezenta in formularul de mai jos. Imaginați-vă. Avem un corp, dar încă nu se poate descrie, știm doar ceea ce particulele sale elementare și modul în care acestea sunt aranjate. În scopul de a colecta corpul într-un întreg, este necesar să se integreze particulelor elementare - pentru a fuziona piese într-un singur sistem. Forma geometrică a funcției y = f (x), integrala este zona delimitată de forma curbei, axa x și 2 linii verticale x = a și x = b.

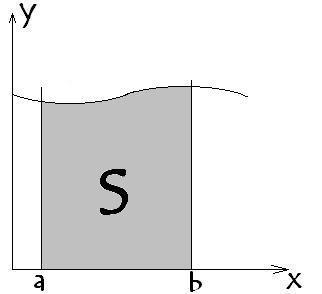
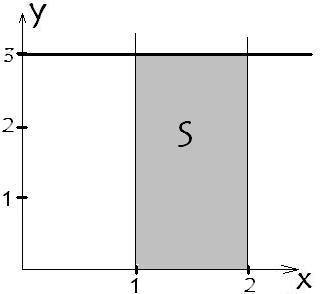
Deci, zona zona hașurată este integrala funcției în intervalul de la A la B. Nu-l crezi? Verificăm pe orice funcție. Ia-un simplu y = 3. Restricționează valori a = 1 și b = 2 funcția. Construit:

Deci, figura dreptunghi mărginit. Zona este produsul din lungimea de lățimea. In cazul nostru, lungime 3 lățime 1, zona 1 * 3 = 3. Să încercăm să rezolve același lucru fără a recurge la construcția, folosind integrarea: După cum se poate vedea răspunsul a fost ca înainte. Integrale SOLUȚIA - adună într-una din orice părți elementare. În cazul benzii suprafață însumate cu o lățime infinitezimal. Integrale pot fi definite și nedefinite. Rezolva mijloacele integrale definite pentru a găsi valoarea funcției în anumite limite. Decizia integralei nedefinită se reduce la găsirea pervoobraznoy.F (x) - primitiv. Diferentierea prototip, vom obține integrandul originală. Pentru a verifica dacă integralei am decis differentsiiruem răspunsul primit și compară cu expresia originală. Principalele funcții și primitivele sunt prezentate în tabelul pentru care:

Tabel primitivelor pentru rezolvarea integralele

Tehnicile de bază de soluții integrale: Solve mijloace proprii pentru a integra funcția variabilei. În cazul în care integrala are o vedere tabel, putem spune că problema cum să rezolve integralei rezolvată. Dacă nu, atunci sarcina principală în rezolvarea integralei devin reducerea acesteia la o vizualizare tabelară. În primul rând, trebuie să vă amintiți proprietățile de bază ale integralelor:

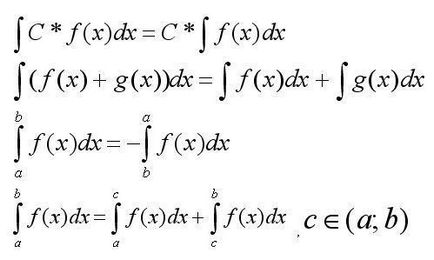
Numai cunoașterea acestor fundamente va permite să rezolve integralele simple. Dar se înțelege că cel mai complex și integral la decizia lor de a recurge la utilizarea unor dispozitive suplimentare. Mai jos ne uităm la câteva exemple de bază de soluții integrale. Receptii va fi dat de orientare generală, fără exemple de soluții. astfel încât să nu supraîncărcați articol. Trebuie să se înțeleagă că în decurs de 5 minute de lectură articol pentru a rezolva toate integralele complexe, nu învață, dar cadru bine formate de înțelegere, va salva de ore de timp pe formarea și dezvoltarea abilităților pentru rezolvarea integralelor.

Tehnicile de bază de soluții integrale

1. Schimbarea variabilă.

Pentru a efectua această tehnică este nevoie de instrumente derivate bune de calificare constatare.

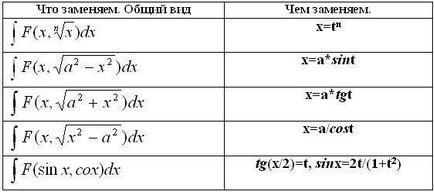
2. Integrarea prin părți. Se utilizează următoarea formulă. Aplicarea acestei formule vă permite să integralele aparent nerezolvabile duce la o soluție.

3. Integrarea funcțiilor raționale. - extinde fracțiunea de prosteyshie- alocă kvadrat.- deplin crea o diferență de la numitor numărător.

4. Integrarea funcțiilor iraționale fracționare. - alocarea la rădăcina unui pătrat complet pentru a crea diferențial în numărătorul pătrat vyvazheniya rădăcină. 5. Integrare Integrare funktsiy.Pri expresii trigonometrice ale formei de formulă se aplică pentru produsul de descompunere. Pentru vyrazheniym-impar, n este orice, vom crea d (cosx). Folosind păcatul de identitate 2 + cos 2 = 1 m, n - chiar, păcatul 2 x = (1-cos2x) / 2 și cos 2 x = (1 + cos2x) / 2 In expresiile formularului: - Aplicare proprietăți tg 2 x = 1 / cos 2 x - 1

1. Pentru a înțelege esența integralelor. Este necesar să se înțeleagă esența de bază a integralei și soluțiile sale. Integral, de fapt, este suma părților elementare ale integrării obiectului. Când este vorba de integrarea funcțiilor, integrala este aria figurii între graficul funcției, axa x și limitele de integrare. În cazul în care nedefinită integrală, și anume, limitele de integrare sunt specificate, decizia vine în jos pentru a găsi pervobraznoy. În cazul integralei definite, este necesar să se înlocuiască valorile limitelor în funcția găsite. 2. Pentru a practica utilizarea tabelului primitivelor și proprietățile de bază ale integralelor. Este necesar să învețe cum să folosească tabelul primitivelor. Pentru o varietate de funcții primitivelor găsit și înregistrate în tabel. Dacă avem integralei, care este în tabel, putem spune că este rezolvată. 3. Pentru a înțelege tehnicile și integralele câștig abilități de rezolvare. În cazul în care integrala nu este sub formă de tabel, soluția sa redus pentru ao aduce în forma unui tabel integralelor. Pentru a face acest lucru, folosim proprietățile de bază ale soluțiilor și tehnici. Dacă în orice etapă de aplicare a metodelor pe care au dificultăți și neînțelegerii, atunci sunt bune în detaliu mai este pe această chitanță, a se vedea exemplele de astfel de plan, întrebați profesorul. În plus, după ce soluția integralei în stadii incipiente, se recomandă să verifice soluția. Pentru a face acest lucru, am differentsiiruem această expresie și compară cu originalul integralei. Evacuare scoate în evidență mai multe exemple:

Exemple de soluții integrale

Exemplul 1: Rezolva integral: nedeterminată Integral. Ne găsim primitiv. Pentru a face acest lucru, vom extinde integrala a sumei în valoare de integralele integralov.Kazhdy sub formă de tabel. Uita-te la primitivele în tabel. Soluție integral: verifica Solution (găsi un derivat):

Exemplul 2. Solve integral indefinit integral. Ne găsim primitiv. Comparați cu masa. Tabel nr. Descompus folosind proprietățile este imposibil. Bucurându-se de recepții. Cea mai mare schimbare corespunzătoare a variabilei. Înlocuiți x + 5 t 5. t 5 = x + 5. Noi primim. Dx dar, de asemenea, trebuie să fie înlocuite cu t. x = t 5 - 5, dx = (t 5 - 5) „= 5t 4. suplean: Integral din tabel. Considerăm: Substituind ca răspuns în loc de t, soluția integrală:

Exemplul 3. Soluție integrală: Pentru a rezolva acest caz, trebuie să selectați un pătrat perfect. selectați:

În acest caz, înainte de koefetsient integral ½ transformat prin înlocuirea dx pe ½ * d (2x + 1). Dacă găsiți derivații x „= 1 și ½ * (2x + 1) = 1, vei înțelege de ce. Ca urmare, ne-am dat parte integrantă a unei tabelara. Ne găsim primitiv.

Ca rezultat, obținem: