Cum de a face felinare chinezești

În prezent, disponibil în comerț de hârtie de culoare de birou, ambele cu o singură față și față-verso. Doar pentru același scop ambalaj adecvat sau hârtie de ambalaj. Dar culoarea obișnuită pentru lecțiile de muncă este mai bine să nu folosească, pentru că este foarte fragil și pauze la locul pliului.

lanterne simple. Ia foaia A4 color, pliere-l în jumătate pe lungime, rigla marca linie la o distanță de 10 mm, nu ajunge la marginea exterioară de 20 mm. Apoi, de-a lungul liniilor de a face incizii și extinde lista. Fold-l în jurul, astfel încât benzile tăiate plasate vertical și lipite împreună margine. aplatiza ușor lanterna rezultată în partea de sus și de jos și coase sau lipici panglica pe care va ține. Puteți face acest tip de produs și inserat în interiorul pliat și lipit baza de o culoare diferită. Aceste lanterne nu pot decora numai pomul de Crăciun și camera, dar, de asemenea, să-și încheie un Crăciun stativ cu lumânări. În cazul în care produc lanterne mici. ele pot fi chiar agățate pe un pai pentru cocktail-uri ca un decor pentru masa.

Felinarele de hîrtie cu figuri. Ia-o jumătate de coală A4 de culoarea selectată, laturile lungi ale dinților tăiate, care sunt apoi necesare pentru lipire cercuri. Harvest siluetele de animale și lipici pe întreaga foaie. Apoi ne întoarcem hârtia într-un tub de lipici și marginile. Se taie hârtia de o diferite cercuri de culoare cu diametru mai mare și lipite de sus și de jos pistoletul cuișoare, rezultând într-o formă bobina. Apoi se întind de ajustare prin firul puternic lanterna și înșirate prin partea de jos 2 cm mai multe puncte colorate, de fiecare dată mai mici. Decoreaza partea de jos a periei firele de culoare, cum ar fi cusut.

lanterne ondulat. În acest scop, este de dorit să se folosească hârtie de ambalaj, deoarece este suficient de lung. Dacă o astfel de hârtie nu este, va avea foile de la lipirea împreună. Semifabricatul de hârtie de măsurare de 20 cm x 60 cm, l ori pe lungime, se va reduce și preforme lungi. Apoi, face din ea este pliat acordeon 1 cm. Dezvăluie prepararea preformei pe întreaga lungime și a stabilit astfel încât acesta semăna acoperișul de la cabină. În această poziție, strângeți fețele sale pe întreaga lungime, rola și sigila marginile. În partea de sus a lanterna pentru a face frânghie pentru agățat. Acesta poate fi atașat la partea de jos a periei tăiate de fir sau animale siluete.

Funcția f (t), în cazul în care t≥0, numit original, în cazul în care: este-continuu sau are porțiuni un număr finit de puncte de discontinuitate a primului tip. La t0, S0> 0, S0 - creșterea originalului).
Fiecare original poate asocia funcția de complexe valori variabile p = s + IW F (p), care este dată de Laplace integrală (vezi. Figura 1) sau o transformare Laplace.

F (p) se numește imaginea funcției inițiale f (t). Pentru fiecare dintre f original (t), iar imaginea există este determinată în jumătate din planul complex Re (p)> S0, unde S0 - funcția indice de creștere f (t).

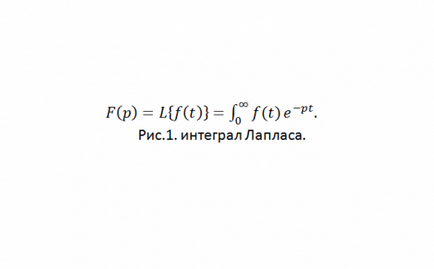
Acum, să ne ia în considerare conceptul de convoluție.

Definiția. Convoluția a două funcții f (t) și g (t), unde t≥0, o nouă caracteristică numită argument t, definit prin expresia (vezi. Fig. 2)

Operația de obținere a convoluție numit funcții de coagulare. Pentru operația de convoluție a îndeplinit toate funcțiile legile de multiplicare. De exemplu, o operație de convoluție are comutativă, adică sinuozitate nu depinde de ordinea în care funcțiile sunt luate f (t) și g (t)
f (t) * g (t) = g (t) * f (t).

Exemplul 1. Se calculează funcția de convoluție f (t) și g (t) = cos (t).
t * costul = int (0-t) (SCO (t-s) ds)

Integrarea expresiei prin părți: u = s, du = ds, dv = cos (t-s) ds, v = -sin (t-s), vei primi:
(-s) sin (t-s) | (0-t) + int (0-t) (sin (t-s) ds = cos (t-s) | (0-s) = 1-cos (t).

Imagine de multiplicare teorema.

Dacă f original (t) este imaginea F (p) și g (t) - G (p), atunci imaginea produsului F (p) G (p) este funcția imagine convoluție f (t) * g (t) = int (0-t) (f (s) g (ts) ds), adică pentru produsul de convoluție a imaginii originale există:
F (p) G (p) =: f (t) * g (t).

înmulțind teorema ne permite să găsim originalul corespunzător produsului a două imagini F1 (p) și F2 (p), în cazul în care sunt cunoscute originalele.

Pentru aceasta există mese speciale și foarte extinse de corespondență și imagini ale originalelor. Aceste tabele sunt disponibile în orice manual matematic.

Exemplul 2. Localizați funcția exp imagine convoluție (t) * sin (t) = int (0-t) (exp (t-s) sin (s) ds).

Conform tabelului de corespondență și imaginea originală la păcatul original (t): = 1 / (p ^ 2 + 1) și exp (t): = 1 / (p-1). Prin urmare, ecranul va avea forma: 1 / ((p ^ 2 + 1) (p-1)).

Exemplul 3. Localizați (disponibil în formă integrată) originală w (t), care imaginea are forma
W (p) = 1 / (5 (p 2)) - (p + 2) / (5 (p ^ 2 + 1), prin transformarea acestei imagini într-un W de lucru (p) = F (p) G (p) .
F (p) G (p) = (1 / (p-2)) (1 / (p ^ 2 + 1)). Conform tabelului corespund cu cele originale și imagini:
1 / (p-2) =: exp (2t), 1 / (p ^ 2 + 1) =: sin (t).

Căutând originală w (t) = exp (2t) * = sint int sint (0-t) (exp (2 (t-s)) sin (s) ds), adică (vezi Fig.3.):