Grafice, exemple și exerciții

Graficele originea în secolul al XVIII-lea, când celebrul mate-Matic, Leonhard Euler, a încercat să rezolve problema acum clasic de poduri Koenigsberg. La acea vreme au existat două Ostrova în legătură cu cele șapte poduri bănci Pregol ale râului și unul cu celălalt în Kenigsber-n așa cum este prezentat în Fig. 7.1. 3adacha cu-în următoarele: să efectueze o plimbare în jurul orașului, astfel încât, după ce trece exact o dată pe fiecare punte de legătură pentru a reveni la același loc de unde a început plimbarea. Rezolvarea acestei probleme, Euler Konigsberg descris ca un grafic, identificând-o cu părțile superioare ale orașului, și marginile - cu poduri, care sunt asociate cu aceste părți. După cum ne arată în § 7.1, Euler a reușit să demonstreze că traseul dorit ocolind orașul nu există.

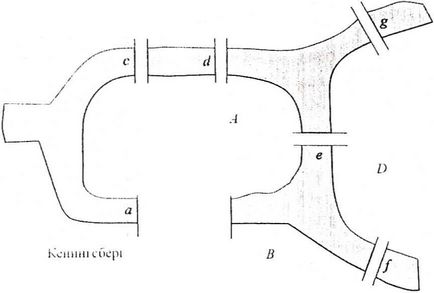
Figura 7.1. Schema vechi Konigsberg

În acest capitol, vom introduce terminologia utilizată în teoria grafurilor, și pentru a înțelege unele sarcini specifice rezolvate cu ajutorul graficelor. În special, ne uităm la clasa de grafice numite copaci. Copaci - model de naturale care reprezintă datele organizate în sistem ierarhic. Căutați copac pentru izolarea obiectelor individuale și de sortare a datelor într-un copac este un punct important de concentrare în informatică. Anexa la acest capitol vom face sortarea și căutarea de date, organizate în copaci.

Fig. 7.1 prezintă cele șapte poduri Konigsberg asa. au fost situate în secolul al XVIII-lea. Problema la care obpa-tilsya Euler, întrebarea este: Putem găsi o cale de mers pe jos, co-Tory se execută o singură dată pe fiecare dintre poduri și începe și se termină în același loc în oraș?

Modelul sarcină - un grafic care constă dintr-o multitudine de vârfuri și o multitudine de muchii care leagă nodurile. Nodurile A, B, C și D simbolizează malul râului și insule, iar marginile o, o. c, d, f și g denotă cele șapte poduri (vezi. fig. 7.2). Căutând traseul (dacă există) corespunde unui circuit de marginile de grafic, astfel încât fiecare dintre ele este trecut doar o singură dată. Extinderea coaste, evident, corespunde intersecției podului râului.

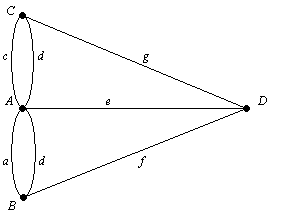
Figura 7.2. modelul de problema podurilor din Königsberg

Grafic în care există o cale, există o cale la rangul și se termină la același vârful și se extinde la toate marginile graficului exact o dată se numește graficul zylerovym. Secvență de anvelope-ver (probabil cu repetiții) prin care trece ISCO-mi traseul ca traseul in sine este numit eylerovymtsiklom. Euler a menționat că, dacă graficul are un ciclu Euler, apoi pentru fiecare muchie, ceea ce duce la unele noduri trebuie să găsească fiecare margine mergând de la vârful 1 și obținut din această nablyudsniya simplu această concluzie: în cazul în care această coloană există ciclu Euler apoi la fiecare vârf trebuie să fie adecvată chiar și numărul de muchii.

In plus, Euler a fost în măsură să dovedească afirmația opusă, Reprezentări, astfel încât graficul în care fiecare pereche de noduri este conectat nu-o secvență de muchii este Euler, dacă și numai dacă toate nodurile sale au chiar grad. Gradul unui vârf v este numărul ö (v) nervurile, se intsidentnyh2.

Acum este clar că graficul modelarea problema podurilor din Königsberg, ciclul Euler nu poate fi găsit. Într-adevăr, dar gradul de nodurile sale sunt impar: δ (B) = δ (C) = δ (D) = 3, și δ (A) = 5. Cu grafice ușor Euler mână, similar cu cel pe care le-am investigat pentru a rezolva problema poduri, utilizare- de oțel în rezolvarea multor probleme practice și de învățare a acestora a crescut într-o zonă importantă de matematică.

grafic simplu este definit ca o pereche G = (V, E), unde V - un set finit de noduri și E - set finit de nervuri, decât poate cuprinde-bucle (muchii, care încep și Zakan-diferențiem un nod) și multiple coaste (numite multiple vayutsya multiple muchii de legătură aceeași pereche de noduri). Graficul prezentat în Fig. 7.2. Nu este simplu, deoarece, de exemplu, nodurile A și B sunt conectate două nervuri (doar aceste margini sunt numite mai multe) pentru a.

Două vârfuri u și v într-un grafic simplu sunt numite adiacente. în cazul în care acestea sunt conectate printr-o margine e. despre care se spune ca ar fi incident de la vârful u (și v). Astfel, putem Reprezentat-vlyat setată E de margini ca un set de perechi de noduri adiacente, definind astfel non-reflexiv, relație simetrică pe V. Lipsa reflexive datorită faptului că într-un grafic simplu nu are bucle, T. E. Reber, ambele capete care sunt în același top. Simetria relației rezultă din faptul că e marginea. Conectarea sus și V, V și se conectează cu și (cu alte cuvinte, nervurile nu sunt orientate, adică. E. Nu au nici o direcție). Marginea de numai un grafic simplu, care conectează o pereche de vârfuri u și v, vom nota cum și v (sau vulgaris).

relație matrice logică pe set de noduri, definit kotopoe marginile sale, numita matrice adiacență. Simetria relațiilor în ceea ce privește matricea de adiacenta M OZNA-chaet că M este simetrică față de diagonala principală. Și din cauza non-reflexivitatea a acestei relații pe diagonala principală a matricei M înseamnă simbolul „L“.

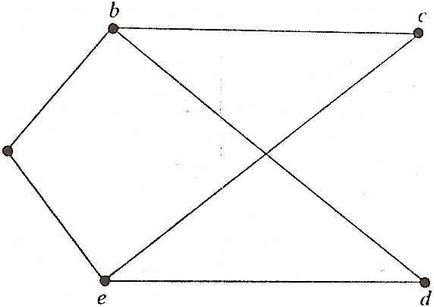
Exemplul 7.1. Desena un grafic G (V, E) cu setul de vârfuri V = și margine set E =. Scrieți matricea sa de adiacență.

Decizie. Un grafic G prezentat în Fig. 7.3.

matricea sa de adiacență este de forma:

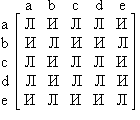
Pentru a restaura graficul avem doar elementele matricei adiacenta, care stau deasupra diagonalei principale.

Subgraf G = (V, E) este graful G '= (V', E '), in care E' C E și V. V „C

Exemplul 7.2: găsi grafice între H, K și L, prezentat în Fig. 7.4 subgrafurilor de G.

Decizie. Notăm nodurile graf G, H și K așa cum se arată în Fig. 7.5. Graficele de H și K - subgrafurilor G, așa cum se vede din notația noastră. Earl L nu este un subgraf al lui G, deoarece acesta este punctul culminant al indicelui 4, iar graficul G nu există o astfel.

Figura 7.9. Un exemplu de grafic hamiltonian

Decizie. Să presupunem că într-un grafic conectat găsi un ciclu hamiltonian. Fiecare nod v este inclus în ciclul hamiltonian cu alegerea a două muchii incidente la ea, și, prin urmare, gradul fiecărui nod din ciclul hamiltonian (după îndepărtarea marginilor superflue) este egal cu 2. Gradul de noduri ale grafului - 2 sau 3. Vârfurile de gradul 2 include un inel împreună cu ambele incidente cu ei coaste. În consecință, muchiile ab, ae, cd, cb, hi, ij hg și într-o anumită ordine include un ciclu C hamiltonian (vezi. Fig. 7.10.).

Bf coaste nu pot face parte din ciclul S. deoarece fiecare vârf al ciclului trebuie să aibă un grad de 2. Deci, coastele și fi fg necesare pentru a intra într-o buclă C. pentru a include vertex f. Dar apoi coaste, iar Gd je nu poate face parte, eventual, la ciclul S., deoarece în caz contrar acesta va fi nodurile de gradul trei. Acest lucru ne obligă să includă în ciclul ed coaste. ceea ce conduce la o contradicție: coaste, am fost forțați să aleagă forma două cicluri deconectate în loc de una, existența pe care ne-am așteptat. Concluzie: Graficul prezentat în figura 7.10, nu este hamiltonian.

grafice Hamiltoniene sunt utilizate pentru modelarea multe probleme practice. Baza tuturor acestor probleme este o problemă clasică de călătorie agent de vânzări.

Agent de vânzări ar trebui să tur orașul și înapoi, după ce a stat în fiecare oraș exact o dată, la reducerea costurilor de călătorie la un nivel minim, în același timp.

Figura 7.10. Nervurile incluse în ciclul hamiltonian C

Modelul grafic al problemei comis-voiajorului este un grafic Hamiltonian, ale cărui noduri reprezintă orașul, și marginile drumului care leagă-le. În plus, fiecare muchie este echipată cu o greutate care indică costurile de transport necesare pentru a călători în mod adecvat, cum ar fi, de exemplu, distanța dintre orașe sau în timpul deplasării pe drum 2. Pentru a rezolva problema, avem nevoie pentru a găsi un ciclu hamiltonian de greutate totală minimă.

cel mai apropiat algoritm vecin.

Acest algoritm produce soluție TSP suboptimal generarea ciclurilor hamiltoniene în coloana încărcată cu o multitudine de vârfuri V. Ciclul rezultat din exploatare a algoritmului, va coincide cu valoarea finală a căii variabile, iar lungimea sa totală - valoarea finală a variabilei w.

whileostayutsya vershinydo nemarcat

Selectați vershinuu nemarcat,

Ca rezultat, algoritmul a fost găsit Hamilton DCABD greutatea totală a buclei 24. Efectuarea unei căutare exhaustivă a tuturor ciclurilor în această cutiuță, puteți găsi alte două ciclu hamiltonian: ABCDA greutate totală de 23 și o greutate totală de ACBDA 31. Graficul complet cu douăzeci de vârfuri există aproximativ 6 1 10 16 cicluri Hamilton, transferul care necesită foarte mult timp și memoria calculatorului.

După cum sa menționat deja, există o clasă de grafice numite arbori, care sunt utilizate în special pe scară largă în aplicații informatice. Un grafic G = (V, E) este numit un copac. dacă este conectat și aciclic (adică. nu conține cicluri).

Fie G = (V, E) - Count nodurile cn și m muchii. Este posibil să se formuleze o serie de condiții necesare și suficiente sub kotoryhGyavlyaetsya copac:

Orice pereche de noduri Gsoedinena singura cale.

Gsvyazen, și îndepărtarea cel puțin una din coastele lui încalcă conectivitatea graficului.

Gatsiklichen, dar dacă adăugați cel puțin o muchie, apoi ciclu vGpoyavitsya.

Echivalența majoritatea acestor condiții sunt stabilite cu ușurință. Cel mai dificil de a face cu a doua dintre ele. În exemplul următor, se arată că un arbore cu n noduri are exact n-1 muchii.

Exemplul 7.7. Dovedeste prin inducție numărul de noduri care derevaT vârfuri și coaste m cn satisface relația: m = n-1.

Decizie. Deoarece copac cu un singur nod nu conține margini, atunci afirmația este adevărată pentru N = 1.

Să considerăm un arbore vârfuri T cn (margini și m), unde n> 1 și presupunem că orice arbore cu k

Scoateți marginea T. A treia derevoT proprietate după această procedură va deveni un grafic deconectat. Obțineți exact două componente conectate, dintre care niciunul nu are cicluri (în caz contrar, grefa original, ar conține prea cicluri și nu ar putea fi un copac). Astfel, componentele conectate - aceleași copaci.

Prin inducerea ipotezei arborelui T1 imeetn1 - 1 coaste AT2-n2 - 1. Ca urmare, derevoT pornire folosește (considerând o telecomandă)

Este ușor de a dovedi că orice grafic conectat există un subgraf, care este un copac. Subgrafic lui G. Este un copac, și include toate vershinyG. copac nazyvaetsyaostovnym. Spanning copac în grafeGstroitsya simplu: alege o muchie arbitrară și adăugați în mod constant celelalte margini, fără a crea un ciclu, atâta timp cât nu va fi adăugarea de margini, fără a obține în acest ciclu. Datorită exemplul 7.7, știm că pentru a construi un copac se întinde în izn grafic picuri trebuie să selectați rovnon - 1 margine.

Exemplul 7.8. Găsiți două copac în diferite Spanning pietriș, prezentat în fig. 7.12.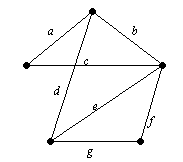

Figura 7.12. Grafic conectat G

Decizie. În acest grafic, există mai multe copaci care acoperă. Una dintre ele este obținut prin selectarea succesivă a muchiilor: a, b, d, ca și f. Altele - b, c, e și g. arbori Chemat sunt prezentate în Figura 7.13.

Procedeul descris în exemplul 7.8 poate fi adaptat pentru cele mai scurte sarcini soluții compuși:

Avem nevoie de a construi o rețea de cale ferată care leagă un număr de orașe. Costul cunoscute de construcție a căilor de segment între fiecare pereche de orașe. Necesar pentru a găsi rețeaua de cost minim.

În limbajul teoriei graficului, trebuie să găsim un arbore grafic încărcat se întinde de cea mai mică greutate totală. Un astfel de copac se numește copac minim se întinde sau, pe scurt MOD. Spre deosebire de problema comis-voiajorului, există un algoritm eficient care găsește într-adevăr arborele minim se întinde. Este similar cu algoritmul Prima.

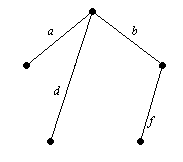
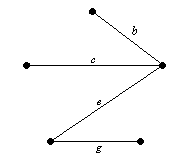
Figura 7.13. G arbori Spanning

Algoritmul de căutare minim Spanning copac. Fie G = (V, E) - conectat grafic ponderat. MOD algoritm construiește un grafic G prin alegerea cea mai mică greutate posibil marginile pentru a forma un arbore de acoperire. MOD este stocată în memoria calculatorului ca o multitudine de muchii T.

e: = rib grafaGs cea mai mică greutate;

Decizie. Nervurile sunt selectate după cum urmează: În primul rând - 1 DE 2 greutate; al doilea - greutate AC 3; al treilea - CE 7. greutatea în acest stadiu sub copac construcție arată ca în Fig. 7,14

Figura 7.14. Vizualizare arborescentă după trei etape

Ar trebui să fie coaste atârnate - AD, AE și CD, fiecare dintre care are o greutate de 9. Cu toate acestea, oricare dintre ele nu am adăugat, rândul său, ciclul. Prin urmare, ar trebui să fie enumerate coaste excluse din construibilă. În continuare vin coaste soare și greutatea BD 11. Puteți atașa oricare dintre ele, în timp ce primește două diferite MOD: greutate sau 23 fiecare.

De multe ori, am dori să avem copaci, care se bazează pe formarea naturală a structurilor ierarhice, cum ar fi, de exemplu, arborele genealogic (ris.7.15). Acesta arată unii membri ai familiei Bernoulli, fiecare dintre ei a fost un celebru matematician elvețian.

Un arbore genealogic poate fi reprezentat mai compact. Schema din figura 7.16 este un exemplu de așa-numitul arbore cu rădăcină. Arbore cu radacina este un arbore cu un nod distins. Este acest vârf dedicat și este rădăcina copacului. Partea de sus a arborelui, situată direct sub rădăcină, sunt numite fii. Pe de altă parte, de sus, în picioare chiar în fața fiului ei chemat pe tatăl ei.