Metoda grafică - programare liniară

Descrierea metodei

Dacă există doar două variabile într-o problemă de programare liniară, atunci acesta poate fi rezolvată prin metode grafice.

Luați în considerare problema programării liniare cu două variabile și.






(1.1);
(1.2)
Aici. există numere de arbitrare. Acest obiectiv poate fi fie pentru găsirea maxim (max), precum și determinarea minim (min). Constrângerile de sistem pot fi prezente ca semne. și semne.

Zona de construcție de soluții fezabile

Metoda grafică pentru rezolvarea problemei (1) după cum urmează.
La început, ne petrecem axele și și selectați scara. Fiecare dintre limitările sistemului inegalităților (1.2) definește semiplanul delimitat de linia dreaptă corespunzătoare.

Deci, prima inegalitate
(1.2.1)
Acesta determină semiplanul delimitat de liniile. Pe de o parte a acestei linii. iar pe de altă parte. La foarte direct. Pentru a afla care parte din inegalitatea (1.2.1), vom alege un punct arbitrar nu pe linie. În continuare, vom înlocui coordonatele acestui punct (1.2.1). În cazul în care inegalitatea este satisfăcută, semiplanul conține punctul selectat. În cazul în care inegalitatea nu este satisfăcută, semiplanul se află pe cealaltă parte (care nu conține punctul selectat). Penumbra, pentru care inegalitatea (1.2.1).

Același lucru se realizează pentru restul sistemului inegalităților (1.2). Deci, vom obține semiplanul umbrite. fezabile puncte din zona soluții satisfac toate inegalitățile (1.2). Prin urmare, grafic, domeniul soluțiilor fezabile (SDT) este intersecția tuturor construite de jumătăți de avioane. SDT umbră. Este un poligon convex a cărei fețe îi aparțin construite din dreapta. SDT, de asemenea, poate fi o nemărginită convex figură, segment, ray sau linie.

Aceasta poate apărea un astfel de caz încât semiplanul fără puncte comune. Apoi, zona de soluții viabile este gol. O astfel de problemă nu are nici o soluție.

Este posibil de a simplifica metoda. Nu poate fi nici o umbrire la fiecare jumătate de plan, și primul care a construi toate directe
(2)
În continuare, pentru a alege un punct arbitrar, nu face parte din nici una din aceste linii. Substitut coordonatele acestui punct în sistemul inegalităților (1.2). În cazul în care toate inegalitățile sunt îndeplinite, atunci regiunea fezabilă este delimitată corect și include construit punctul selectat. Shade regiunea fezabilă pentru frontiere directe, astfel încât acesta include punctul selectat.

Dacă oricare condiție nu este îndeplinită, atunci alege un alt punct. Și așa mai departe, până când se găsește un punct, coordonatele care satisfac (1.2).

Găsirea extremum funcției obiectiv

Deci, avem o zonă umbrită de soluții fezabile (TSD). Este limitat de linia poligonala aparținând liniilor drepte construite și constând din grinzi (2). SDT este întotdeauna convexă. Acesta poate fi un set mărginit, și nu limitat de-a lungul unor direcții.

Acum ne putem uita pentru o extremum a funcției obiectiv
(1.1).

Pentru a face acest lucru, alege orice număr și de a construi directe
(3).
Din motive de comoditate în continuare noi credem că această linie trece prin SDT. Pe această linie funcția obiectiv este constantă și egală. această linie se numește funcțiile la nivel de linie. Această linie împarte planul în două jumătăți de avioane. Pe de o jumătate de avion
.
Pe de altă semiplanul
.
Aceasta este, pe de o parte a liniei (3) funcția obiectiv crește. Și în continuare am otodvinem punct din linia (3), cu atât mai mare valoarea. Pe de cealaltă parte a liniei (3) funcția obiectiv este în scădere. Și în continuare am otodvinem punct din linia (3), în cealaltă direcție, cea mai mică valoare. Dacă vom trage o linie paralelă cu linia (3), noua linie va conduce, de asemenea, nivelul funcției obiectiv, dar cu o valoare diferită.

Astfel, pentru a găsi valoarea maximă a funcției obiectiv, este necesar să se traseze o linie dreaptă paralelă cu linia (3), distanța maximă față de ea în direcția creșterii valorilor. și extinzându-se prin cel puțin un punct din SDT. Pentru a găsi valoarea minimă a funcției obiectiv, este necesar să se traseze o linie dreaptă paralelă cu linia (3) și o distanță maximă față de ea în direcția valorilor descrescătoare. și extinzându-se prin cel puțin un punct din SDT.

Dacă SDT este nelimitată, poate exista un caz în care o linie dreaptă nu poate deține. Aceasta este, indiferent de modul în care au fost eliminate în mod direct de la nivelul liniei (3), în direcția de creștere (scădere). atunci linia va trece întotdeauna prin SDT. În acest caz, poate fi arbitrar de mare (mici). Prin urmare, valoarea maximă (minimă) din nr. ceea ce face problema nu.

Să considerăm cazul în care o linie paralelă extremă la orice linie a formei (3), trece printr-unul dintre nodurile SDT poligon. Din grafic determinăm coordonatele nodurilor. Apoi, valoarea maximă (minimă) a funcției obiectiv este dată de:






.
soluție a problemei este
.

Se poate întâlni, de asemenea, cazul în care linia este paralelă cu una dintre fețele SDT. Apoi, linia trece prin două vârfuri ale SDT poligon. Și determină coordonatele acestor noduri. Pentru a determina valoarea maximă (minimă) a funcției obiectiv, este posibil să se utilizeze oricare dintre aceste coordonate de noduri:
.
Problema are infinit mai multe soluții. Soluția trebuie să fie orice punct situat pe segmentul dintre punctele și. inclusiv punctele ei înșiși și.

Un exemplu de rezolvare a problemei metodei grafice de programare liniară

problemă condiție

Compania produce o rochie două modele A și B. Utilizarea a trei tipuri de tesut. La fabricarea unui model de rochie A necesita 2 m de primul tip de țesătură, țesătura 1 m al doilea tip, 2m al treilea tip de tesut. La fabricarea unui model de rochie este necesară în tesatura 3 m de primul tip, m-1 a doua forma de tesatura de 2 m al treilea tip de tesut. Stocurile de primul tip de material este de 21 m, a doua specie - 10 m, al treilea tip. - 16 m Issue un singur tip de produs A generează venituri 400 den. u un singur tip de produs B - 300 den. u

Creați un plan de producție, care oferă companiei cele mai mari venituri. Problema rezolvată prin metode grafice.

Să variabilele și înseamnă cantitatea de rochii modele A și B, respectiv. Apoi, suma cheltuită primul tip de țesut este:
(M)
Volumul utilizat al doilea tip de țesut este:
(M)
Volumul utilizat al treilea tip de tesatura va fi:
(M)
Deoarece cantitatea produsă de rochii nu poate fi negativ, atunci
și.
Veniturile din taxa se va face:
(Den. Unități).

Apoi, modelul economic și matematic al problemei este după cum urmează:

Rezolvăm metoda grafică.
Desenați axe de coordonate.

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă care trece prin punctul (0, 7) și (10,5, 0).

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă care trece prin punctul (0, 10) și (10, 0).

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă prin punctele (0, 8) și (8, 0).

Directă și sunt axe de coordonate.

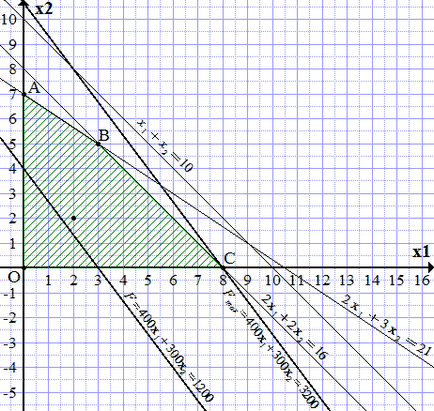
soluții fezabile FIELD (SDT) este delimitată de liniile construite și axele de coordonate. Pentru a afla care parte, vom vedea că punctul aparține SDT, astfel cum satisface sistemul de inegalități:

Zona Shade la punctul (2, 2) a lovit porțiunea eclozat. Obținem OABC patrulater.

Construirea liniei nivel arbitrar al funcției obiectiv, de exemplu,
(A1.1).
Când.
Când.
Trage o linie dreaptă care trece prin punctul (0, 4) și (3, 0).

În continuare observăm că, din moment ce coeficienții pozitiv și funcția țintă (400 și 300), crește cu u. O linie dreaptă este paralelă cu maximă Distanța de la ea în direcția creșterii liniei (A1.1). și extinzându-se prin cel puțin un punct al unui OABC patrulater. O astfel de linie dreaptă trece prin punctul C. Din construcția defini coordonatele sale.
.

Asta este, pentru a câștiga cele mai multe venituri, aveți nevoie pentru a face rochii de 8 Modelul A. Venitul va ajunge apoi 3,200 den. u

problemă condiție

Pentru a rezolva problemele de programare liniară prin metode grafice.

Rezolvăm metoda grafică.
Desenați axe de coordonate.

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă prin punctele (0, 6) și (6 0).

Construirea unei linii drepte.
Aici.
Când.
Când.
Trage o linie dreaptă care trece prin punctul (3, 0) și (7, 2).

Construirea unei linii drepte.
Construirea unei linii drepte (axa x).

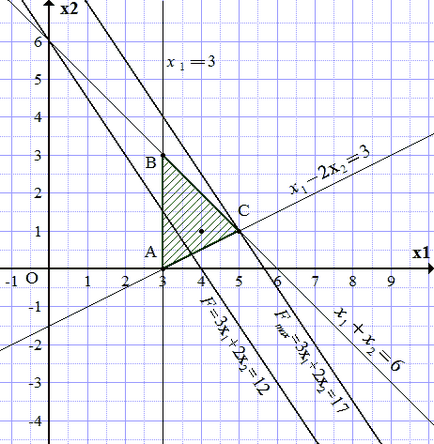
soluții fezabile FIELD (SDT) este delimitată direct construită. Pentru a afla care parte, vom vedea că punctul aparține SDT, astfel cum satisface sistemul de inegalități:

Zona umbrirea pe frontierele construite linii drepte la un punct (4; 1) a lovit porțiunea hașurată. Obținem triunghiul ABC.

Construirea liniei nivel arbitrar al funcției obiectiv, de exemplu,
.
Când.
Când.
Trage o linie dreaptă prin nivelul punctului (0, 6) și (4 0).
Deoarece funcția obiectiv crește cu și. vom trage o linie paralelă cu nivelul liniei, iar distanța maximă de la ea, în direcția de creștere. și extinzându-se prin cel puțin un punct al triunghiului AVC. O astfel de linie dreaptă trece prin punctul C. Din construcția defini coordonatele sale.
.

Un exemplu de lipsa de soluții

problemă condiție

Rezolva problema de programare liniară grafic. Găsiți valoarea maximă și minimă a funcției obiectiv.

Noi rezolva problema metodei grafice.
Desenați axe de coordonate.

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă prin punctele (0, 8) și (2,667, 0).

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă prin punctele (0, 3) și (6 0).

Construirea unei linii drepte.
Când.
Când.
Trage o linie dreaptă care trece prin punctul (3, 0) și (6, 3).

Directă și sunt axe de coordonate.

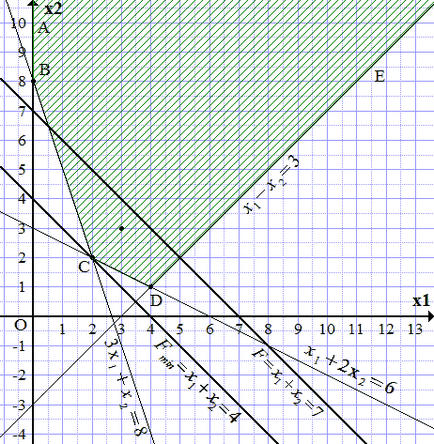
soluții fezabile FIELD (SDT) este delimitată de liniile construite și axele de coordonate. Pentru a afla care parte, vom vedea că punctul aparține SDT, astfel cum satisface sistemul de inegalități:

Zona Shade la punctul (3, 3) este împinsă în porțiunea umbrită. Obțineți domeniu nelimitat delimitat de linia ABCDE rupt.

Construirea liniei nivel arbitrar al funcției obiectiv, de exemplu,
(A3.1).
Când.
Când.
Trage o linie dreaptă prin punctele (0, 7) și (7, 0).
Deoarece coeficienții pentru pozitive și apoi crește odată cu creșterea și.

Pentru a găsi maxim, aveți nevoie pentru a trage o linie paralelă, cea mai telecomanda în direcția de creștere. și extinzându-se prin cel puțin un punct din zona ABCDE. Cu toate acestea, deoarece zona este nelimitat de valorile ridicate și. că un astfel de comportament nu poate fi drepte. Oricare ar fi linia care nu le-am efectuat, vor exista întotdeauna zona unui punct mai îndepărtat în direcția de creștere și. Prin urmare, nu există nici un maxim. Ea poate fi făcută în mod arbitrar.

Cautam cel puțin. O linie dreaptă este paralelă cu linia (A3.1) și cele mai îndepărtate de aceasta, în direcția de scădere. și extinzându-se prin cel puțin un punct din zona ABCDE. O astfel de linie dreaptă trece prin punctul C. Din construcția defini coordonatele sale.
.
Valoarea minimă a funcției obiectiv:

Valoarea maximă nu există.
valoarea minimă
.