Metoda matricei de sisteme de ecuații liniare de rezolvare (solutie Slough folosind o matrice inversă)
În acest articol, hai sa vorbim despre metoda de matrice pentru sisteme de ecuații algebrice liniare ale formei de rezolvare
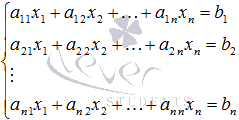
Mai întâi descriem esența metodei de matrice, să ne ia în considerare starea de aplicabilitate a acestei metode, mai în detaliu analiza soluțiile de mai multe exemple.
Navigare în pagină.
Metoda matricei de sisteme de ecuații algebrice liniare de rezolvare - derivare.
Să presupunem că o matrice inversă a matricei A de ordinul n a n. Înmulțind ambele părți ale partea stângă a ecuației matricei (comenzi matrici A ⋅ X și B permite să facă această operație, consultați operațiile de articol pe matrici, proprietăți de operații). Avem. Deoarece pentru funcționarea multiplicarea matricilor adecvate ordine asociativitatea proprietate caracteristică, acesta din urmă Ecuația poate fi rescrisă ca și prin definiție matricea inversă (E - matricea identitate de ordinul n a n), așa
Astfel, soluția sistemului de ecuații liniare prin metoda matricei este determinată prin formula. Cu alte cuvinte, soluția este SLAE folosind matricea inversă.
Știm că o matrice pătrată A de ordinul n cu n matrice are un invers numai dacă determinantul său nu este zero. Prin urmare, un sistem de n ecuații liniare algebrice cu metoda de matrice n Necunoscute poate fi rezolvată numai dacă determinantul sistemului cu matrice principal este nenul.
Exemple de sisteme de ecuații liniare folosind metoda matricei de rezolvare.
Să considerăm o metodă de matrice de exemplu. În unele cazuri, nu vom descrie în detaliu procesul de calcul determinanții matrici, dacă este necesar, consultați articolul, calcularea determinantului matricei.
Sistemul de ecuații în formă de matrice este. Calculăm determinantul matricei principale a sistemului și asigurați-vă că acesta este diferit de zero:
polinom pătratic nu este egal cu zero, sub orice valori reale, deoarece discriminantă său este negativ, astfel încât principalul factor determinant al sistemului de matrice nu este egal cu zero, în conformitate cu orice titlu valabil. Prin metode de matrice avem. Noi construim matricea inversă prin formula:

Vă recomandăm să verificați rezultatul.
.
Metoda matricei de rezolvare a sistemelor liniare, în care numărul de ecuații este egal cu numărul de variabile necunoscute și determinantul matricei principală a sistemului este diferit de zero. În cazul în care sistemul conține mai mult de trei ecuații, găsirea matricea inversă necesită un efort considerabil de calcul, astfel încât în acest caz, este recomandabil să se folosească metoda pentru a rezolva Gauss.