Multimi fuzzy și caracteristicile lor
Fuzzy (sau neclară, neclare) set - noțiune de Zadeh LA, care sa extins clasic (Cantor) set concept, presupunând că funcția caracteristică (apartenența elementului funcția set) poate lua orice valoare în intervalul [0,1], și nu numai valorile 0 sau 1.
Definiția. mulțimea fuzzy (un set neclare)
Fie C un set universal (universul). Apoi mulțimea fuzzy A la C este definit ca un set ordonat de perechi
unde se numește funcția de membru (AF) a unui element x la mulțimea fuzzy A.
AF atribuie fiecărui element al valorii C în intervalul [0, 1], care se numește gradul de apartenență al X la A sau măsură fuzzy.
Fuzzy măsură poate fi considerată ca un grad de adevăr că elementul x apartine lui A.
Definiția. bazat pe mulțimi fuzzy (un suport al unei fuzzyset)
Un set fuzzy este un set de puncte astfel încât.
Astfel, definiția multimilor fuzzy este o extensie a setului definiție clasică, în care funcția caracteristică poate lua valori continue între 0 și 1. Universul C poate fi set discret sau continuu.
Pentru reprezentarea AF este utilizat, de obicei, mai multe tipuri de funcții parametrice.
Prezentarea tipică a AF
OP triunghiulara (. Figura 2.2 a) descrie trei parametrii a, b, c>, care determină x coordonate ale celor trei unghiuri ale triunghiului, după cum urmează:
(. Figura 2.2 c) Trapezoidal OP sunt descrise de patru parametri a, b, c, d>, care determină coordonatele x cele patru colțuri ale trapezului, după cum urmează:
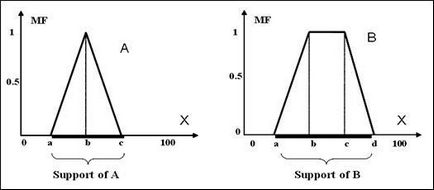
Fig. 2.2. OP triunghiulara și trapezoidală
OP Gaussian (. Figura 2.3) sunt specificate de doi parametri și reprezintă următoarea funcție.
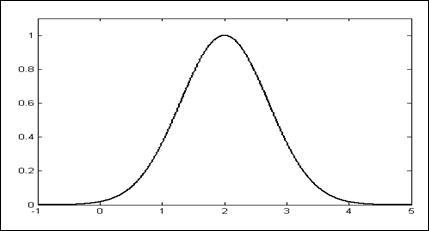
Fig. 2.3. OP Gaussian
Unul dintre conceptele fundamentale introduse ca Zadeh, este conceptul de variabilă lingvistică.
Definiția. variabilă lingvistică (PL) reprezintă următoarele cinci. unde - numele variabilei - termenul stabilit, având în vedere un set de valori LP sunt expresii lingvistice (sintagmele), X - univers, G - regula sintactic, folosind care putem forma o sintagmă. M - regula semantica folosind fiecare sintagmă este atribuită valoarea sa, care este un set neclar în X. univers
Un exemplu al PL poate fi, de exemplu, variabila = „vârstă“. set Termenul ei poate fi, de exemplu, după cum urmează:
(Age) = foarte tânără. tânără. mai mult sau mai puțin tânăr. De vârstă mijlocie. vechi. foarte vechi>.
Pentru acest univers LP poate servi ca un set de numere reale, de exemplu, intervalul. M atribuie Termele reguli semantice ale valorilor T (vechi), care sunt diferite modificări ale mulțimilor fuzzy.
Revenind la exemplul nostru, controlul mișcării vehiculului și să descrie valorile lingvistice în regulile de mai sus, folosind seturile fuzzy. Luați în considerare următoarele variabile lingvistice:
x - distanța între vehicule;
y - echitatie masina de viteză înainte;
Z - accelerației vehiculului gestionat.
AF ar trebui să fie determinată în conformitate cu controlul considerat a situației. De exemplu, o viteză de 70 km / oră este „mare“, în situația de trafic pe drum și orașul poate fi considerat ca fiind „mici“, în situația traficului pe autostradă.
Noi definim de exemplul nostru, următoarele universuri:
Fig. 2.4 OP demonstrat pentru a descrie valorile lingvistice „mici» (lent) și „mare» (rapid) pentru viteza si „aproape» (scurt) și „mare» (lung) pentru distanța.
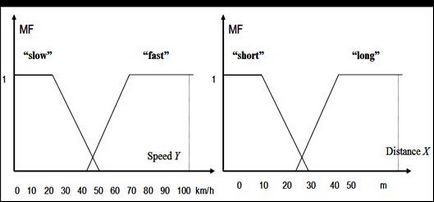
Fig. 2.4. Multimi fuzzy pentru sarcini de control al mișcării simplu de vehicule
Diferențele între reprezentarea clasică și mulțimi fuzzy
Să discutăm aceste diferențe, cu următorul exemplu. Luați în considerare reprezentările set clasice și fuzzy, pentru a descrie valorile lingvistice „scurt“ (pentru distanta).
Fig. 2.5 arată diferențele dintre clasic și reprezentarea fuzzy a unei multitudini de A pentru acest exemplu.
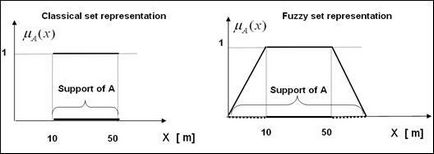
Fig. 2.5. reprezentări clasice și fuzzy a multimii A
Definim o reprezentare clasică a multimii A, așa cum este prezentat în Fig. 2.5 din stânga. În acest caz, funcția caracteristică este:
O reprezentare a seturilor fuzzy, prezentate în Fig. 2.5 pe dreapta. În acest caz, AF funcționează accesorii, după cum urmează:
Acum pune întrebarea următoare. dacă punctul aparține m sau punctul de m mnozhestvuA?
Din punctul de vedere al reprezentării clasice a răspunsul este „nu“. Din punct de vedere al percepției umane, mai degrabă răspunde „da“ decât „nu“. Din punct de vedere al reprezentării fuzzy a răspunsul este „da“.
Astfel, acest exemplu simplu demonstrează că o abordare neclară mai aproape de natural, uman, și este mai flexibilă decât abordarea clasică.
Cu ajutorul mulțimilor fuzzy, putem descrie limitele neclare.
Operații de bază în teoria mulțimilor fuzzy
Definim operația neclară de bază urmează.
Definiție: Un subset neclar (retenție fuzzy sau subsetul fuzzy). Un set fuzzy conținută într-un set neclare B (sau echivalent, A este un subset al B) dacă și numai dacă pentru toți. În formă simbolică:
Definiție: Echivalența mulțimi fuzzy (Egalitatea de seturi fuzzy). Echivalența (egalitatea) mulțimi fuzzy A și B este definită după cum urmează:
Definiție: unire neclară sau disjuncție neclară (fuzzy Union) .Obedinenie două mulțimi fuzzy A și B (în formă simbolică sau scrisă ca A sau B sau A B) este un set fuzzy. AF este definită după cum urmează:
Definiție: intersecția neclară (Intersecția fuzzy) intersecție a două seturi fuzzy, descendent A și B (în formă simbolică sau scrisă ca C = A și B. sau C = A B.) Au un set fuzzy. AF este definită după cum urmează:
Definiție: o adăugare neclare. Supliment A (simbolic scrisă sau) este neclară, AF se determină după cum urmează:
Figura 2.6 prezintă exemple de operații asupra fuzzy, seturile fuzzy.
Fig. 2.6. Exemple de operații neclară pe mulțimi fuzzy
Caracteristici ale mulțimilor fuzzy
Notă caracteristicile importante ale teoriei mulțimilor fuzzy.
1) Legea mijloc exclus și kontradiktsii legii. în cazul în care - adevărat la setul gol în teoria mulțimilor clasice, dar teoria mulțimilor fuzzy, în general, acestea nu sunt îndeplinite.
Drept mijloc exclus și kontradiktsii drept în teoria fuzzy este după cum urmează: și.
2) O multitudine de clasic set teoretic dot poate avea una din cele două posibilități: sau. La punctul teoretic neclare pot aparține mulțimea A, și simultan aparțin A (adică aparțin setului) cu diferite valori ale funcțiilor de membru și. așa cum se arată în Fig. 2.7.
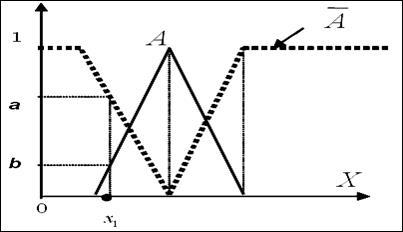
Fig. 2.7. Caracteristica de mulțimi fuzzy
Acest lucru înseamnă că, în procesul de raționament neclare, putem lua în considerare simultan două posibilități, ceea ce face ca procesul de motivare mai flexibilă decât clasic.
3) Relația cu teoria probabilității. Teoria mulțimilor fuzzy într-un anumit sens, se reduce la teoria seturilor aleatoare, și astfel la teoria probabilității. DESCRIERE Teoria SECVENȚE descrie această reducere, se află în afara domeniului de aplicare al acestei cărți [vezi. Link-uri către site-ul Wikipedia]. Ideea de bază este aceea că valoarea funcției de membru poate fi considerată ca probabilitatea elementului de acoperire pentru un anumit set B. aleatoare Cu toate acestea, în aplicarea practică a aparatului de teoria mulțimilor fuzzy este de obicei folosit singur, vorbind la competitorul aparatul teoriei probabilităților și statistică aplicată.