Număr de serie

1. Concepte de bază

Să u1, u2. U3. ..., ONU. ...  șir infinit de numere. expresie

nazyvaetsyabeskonechnym seria numerică. Numărul u1, u2. U3. ..., membrii ONU  ai seriei; Acesta a solicitat un termen general al seriei. Câteva adesea scrise în formă prescurtată (pliat):

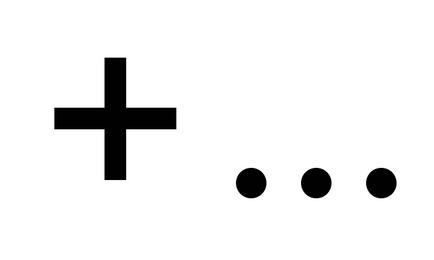
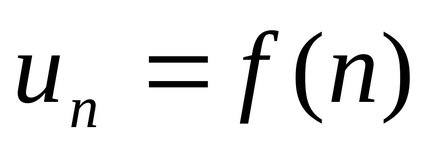
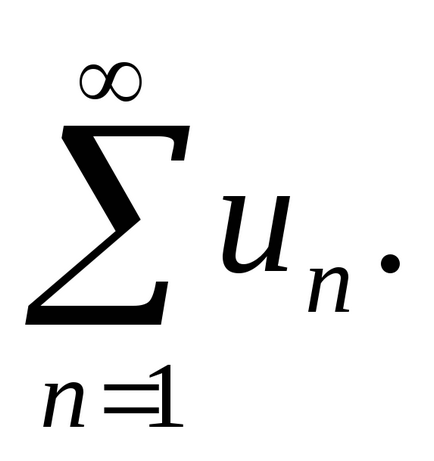
Suma primilor n membri ai unei serii de numere notate

și nazyvayutn mii sumă parțială a seriei:

.

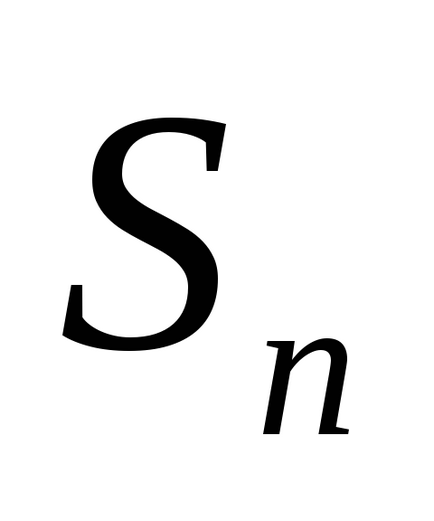
Seria se numește convergentă. în cazul în care suma parțială a n-

vozrastaniin unconfined se apropie de o limită finită, adică, dacă numărnazyvayutsummoy serie.

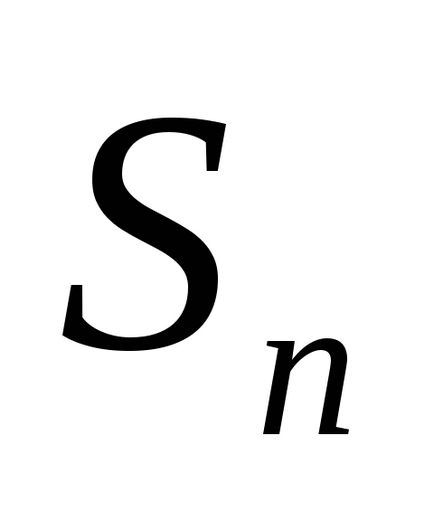
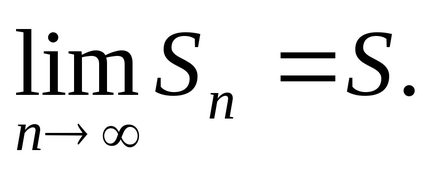
În cazul în care suma parțială n-lea al seriei de la

Ea nu tinde să o limită finită, numărul de nazyvayutraskhodyaschimsya.

Exemplul 1. Găsiți suma seriei.

Decizie. avem

. Deoarece:

,

.

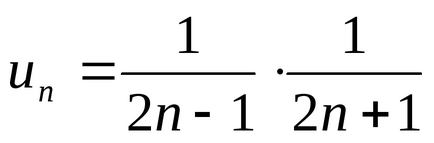
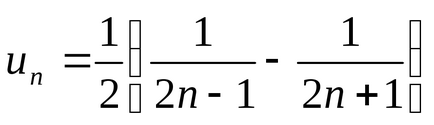
De atunci seria converge și suma acesteia este

.

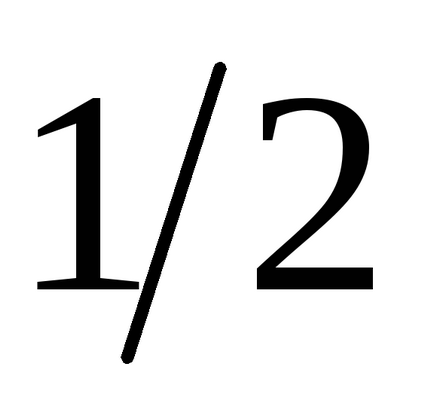
2. Principalele Teoremele pe seria numerică

Teorema 1. În cazul în care seria

convergența serieicare rezultă din aruncarea unui număr de primmembrii (ultimul număr apelat-m rest serie original). Pe de altă parte, convergența-lea restul seriei presupune convergența seriei.

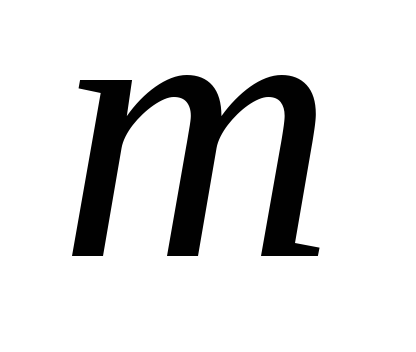
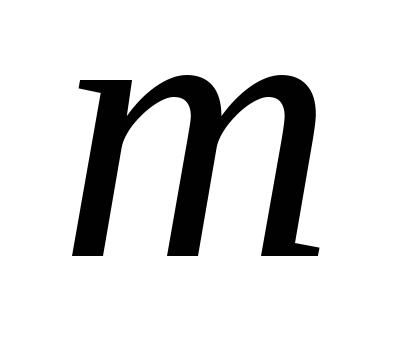
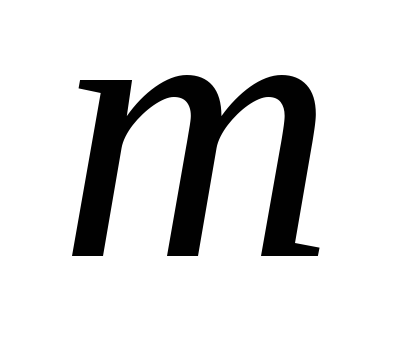
Teorema 2. În cazul în care seria și este suma numărului de

, apoi converge sumă ryadprichem egală cu ultimul rând.

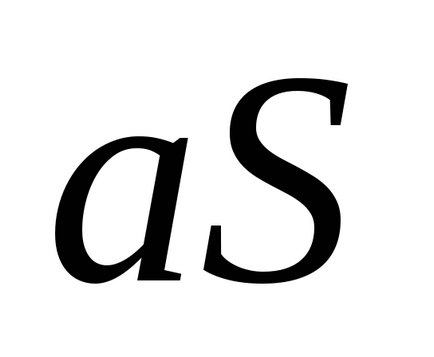
Teorema 3. Dacă sunteți de acord cu rânduri, respectiv summyS și Q, a converge seria și suma este egală cu ultimul rând

.

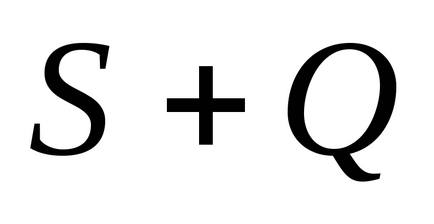
Teorema 4 (necesară pentru convergența seriilor). În cazul în care seria converge,

, și anume lalimită a numărului total de membri convergente este zero.

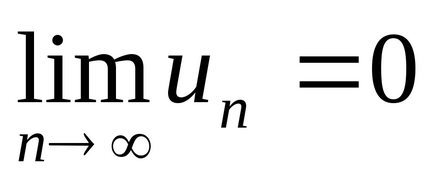
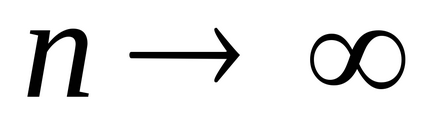
Corolarul 1. Dacă

, atunci seria este divergenta.

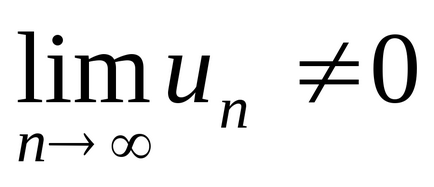
Corolarul 2. Dacă

, apoi determină convergența sau divergența seriei cu ajutorul criteriului de convergență necesare nu ar trebui să fie. Un număr poate atât convergente și divergente.

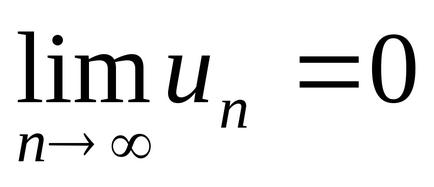
Exemplul 2. Se examinează convergența seriilor:

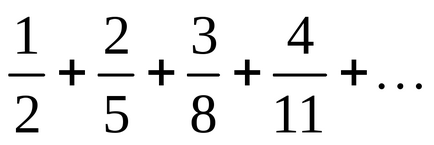
Decizie. Găsiți termenul general al seriei. Deoarece:

,

și anume

, apoi diverge seria (nu deține condiția necesară pentru convergență).

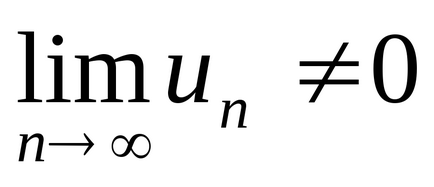
3. Semne de convergenta seriilor cu termeni pozitivi

3.1. test de comparație directă

test de comparare directă pe baza unei comparații a unui număr predeterminat de convergență, cu un număr de convergență sau divergență care este cunoscută. Pentru comparație, folosind seria de mai jos enumerate.

rând

compus din membri ai oricărei progresie geometrică în scădere este convergent și are o sumă

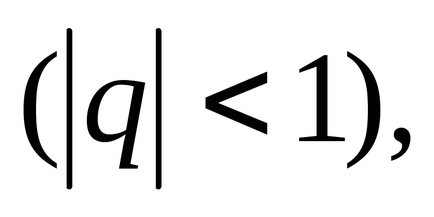
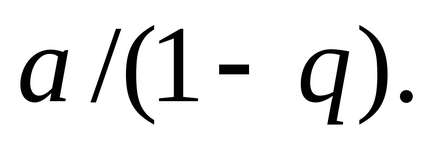
rând

compus din membri care cresc exponențial, este divergentă.

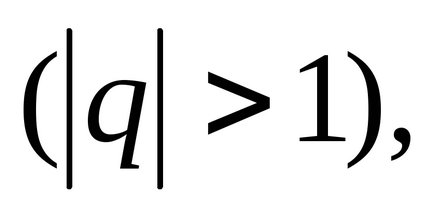
rând

Este divergent.

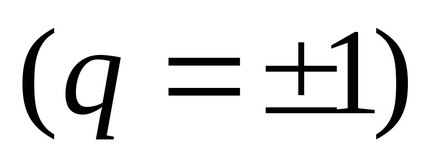
Seria se numește o serie Dirichlet. Pri> 1 seria Dirichlet converge la <1- расходится.

Când  = 1 serie

Se numește armonic. Seria armonică divergenta.

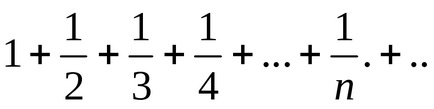
Teorema. Primul semn al comparației. două serii cu termeni pozitivi Să presupunem că:

în care fiecare membru al seriei (1) nu depășește numărul corespunzător de membri (2), adică

(N = 1, 2, 3, ...). Apoi, dacă seria (2), convergența seriilor (1); Dacă intervalul debit (1), varianța și seria (2).

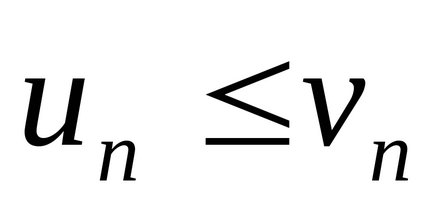
Notă. Această caracteristică rămâne în vigoare în cazul în care neravenstvo

Nu este efectuată pentru toți, ci numai pornind de la un anumit numărn = N. și anume toate nN.

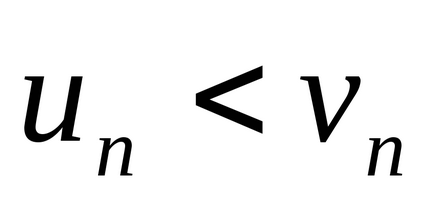
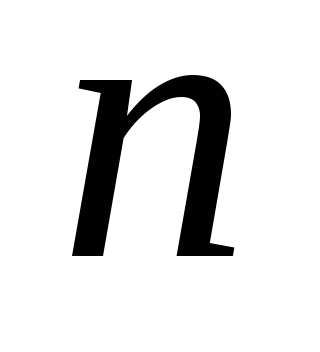
Exemplul 3. Pentru a investiga convergența

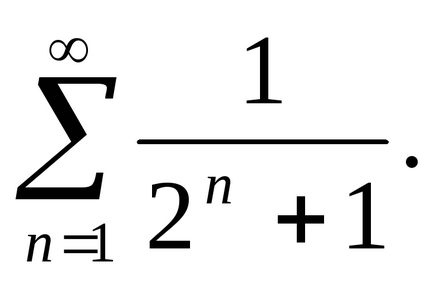
Decizie. Membrii din seria mai puțin decât condițiile corespunzătoare ale seriei

compus din membri ai progresiei geometrice infinite. Din moment ce această serie converge, apoi converge și având în vedere un număr.

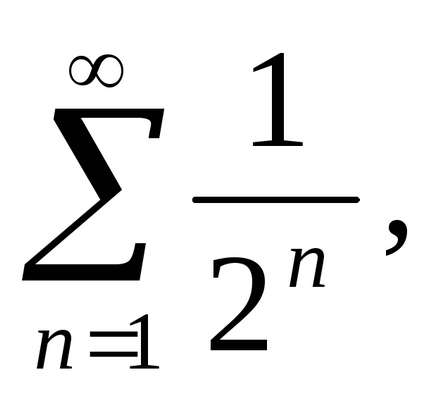
Teorema. A doua caracteristică comparație (testul de comparație a limita forma). Dacă există o limită finită și nenulă

, atunci ambele seriișiconverg sau diverg simultan.

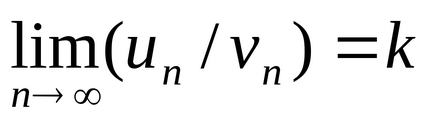
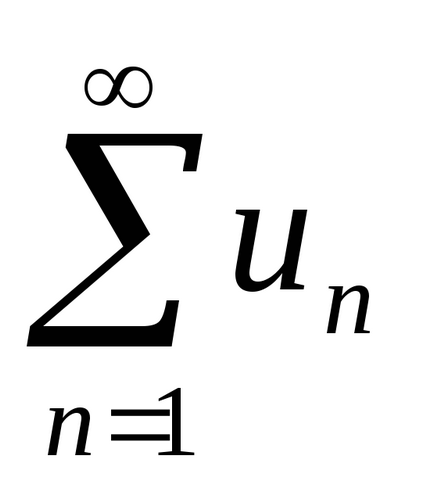
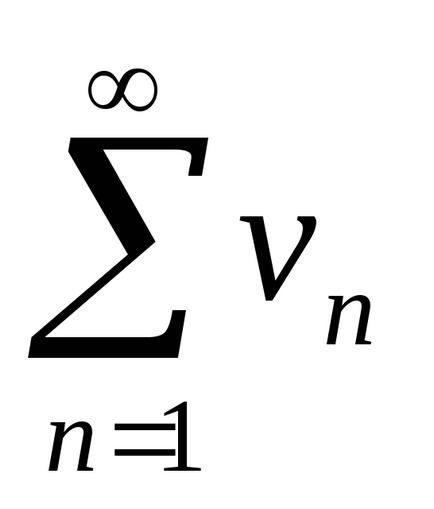
Exemplul 4. Pentru a investiga convergența

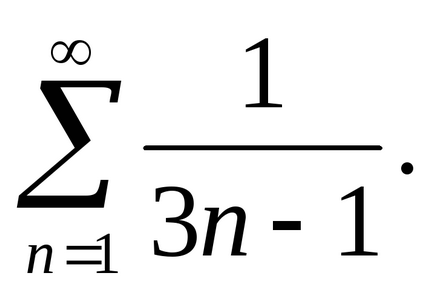
Decizie. Comparabil cu numărul seriei armonice

Am găsit limita raportului dintre termeni generali ai seriei:

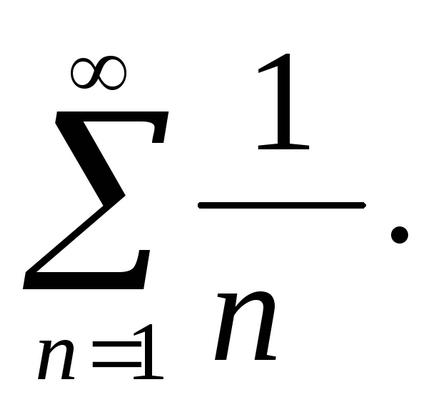
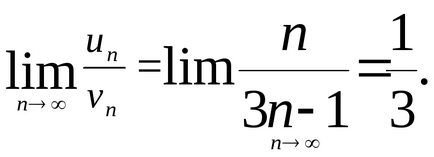
Deoarece seria armonică divergenta, apoi divergent și având în vedere un număr.