Proprietățile sinus, cosinus, tangentă și cotangentă unghiului

Definițiile sinus, cosinus, tangenta și cotangentă unghiului permite setarea unui număr de rezultate specifice - proprietățile sinus, cosinus, tangentă și cotangentă. În acest articol ne uităm la trei proprietăți principale. Primul dintre aceste puncte sinusale unghi semne, cosinus, tangentă și cotangentă alfa în funcție de unghiul de coordonate sfert este α. În continuare, considerăm proprietatea periodicitate, stabilește imutabilitatea valorii sinus, cosinus, tangentă și cotangentă unghiului α atunci când schimbă acest unghi printr-un număr întreg de rotații. A treia proprietate arată o relație între valorile sinus, cosinus, tangentă și cotangentă unghiurile opuse a și -α.

Dacă sunteți interesat de proprietățile funcțiilor sinus, cosinus, tangentă și cotangentă, acestea pot fi studiate în secțiunea corespunzătoare a articolului funcțiile elementare de bază și proprietățile și graficele lor.

Navigare în pagină.

Semne de sinus, cosinus, tangentă și cotangentă de sferturi

Mai târziu, în acest paragraf se va produce termeni „unghiul I. II. III și IV coordonate trimestru“. Noi explica ce fel de colțuri.

Ia cercul unitate. Trebuie remarcat, la punctul de pornire A (1, 0). și rotiți în jurul punctul O, cu un unghi α. în acest caz, presupunem că vom ajunge la punctul A1 (x, y).

Se spune că unghiul a este unghiul I. II. III. IV coordonate trimestru. în cazul în care A1 se află în I. II. III. IV sferturi respectiv; dacă unghiul a este de așa natură încât A1 se află pe oricare dintre liniile de coordonate Ox și Oy. atunci acest unghi nu aparține uneia dintre cele patru trimestre.

Pentru claritate, vom da o ilustrare grafică. In desenele de mai jos arată unghiurile de rotație 30. -210. 585 și -45 de grade, care sunt unghiurile I. II. III și IV coordonatei sferturi respectiv.

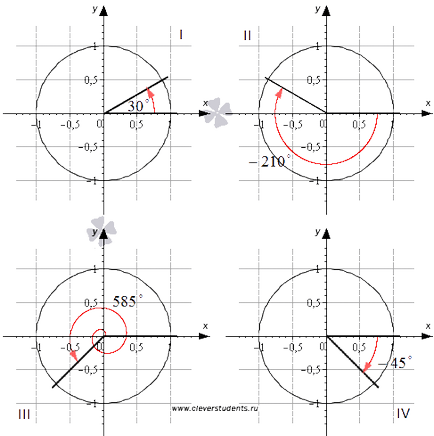
Unghiuri de 0, ± 90, ± 180, ± 270, ± 360, ... grade nu aparține nici uneia dintre coordonate trimestre.

Acum vom înțelege, ce semnele sunt unghiul alfa sinus, cosinus, tangentă și cotangentă de rotație în funcție de un unghi care este de un sfert de α.

Pentru sinus și cosinus pentru a face acest lucru, pur și simplu.

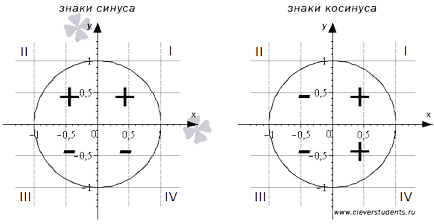
Prin definiție, sinusul unghiului a - este ordonata punctului A1. Evident, în zonele I și II sferturi de coordonate este pozitiv, iar în cadranele III și IV - negativ. Astfel, sinusul unghiului a este pozitiv în cadranele I și II, iar semnul minus - în cadranele III și VI.

La rândul său, cosinusul unghiului a - este abscisa punctului A1. În cadranele I și IV este pozitiv, iar în cadranele II și III - negativ. În consecință, valorile cosinusul unghiului a din cadranele I și IV sunt pozitive, iar în cadranele II și III - negativ.

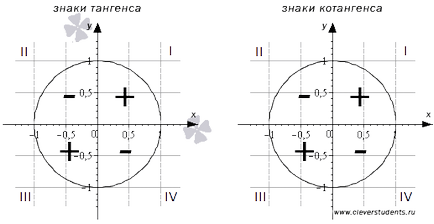
Pentru a identifica semnele de trimestre tangentă și cotangentă trebuie să-și amintească definițiile lor: - este linii electroaprovizionare raportul dintre ordonatele punctul A1 la abscisă și patutului - raportul dintre abscisa la punctul ordonatei A1. Apoi, regulile de diviziune a numerelor cu aceleași și diferite semne, rezultă că tangenta și cotangentă au un semn plus, atunci când abscisa și ordonata marchează punctul A1 sunt aceleași, și au un semn minus - ca abscisă și marchează ordonata punctul A1 este diferit. În consecință, tangenta și cotangentă unghiului sunt în + I și III coordonează sferturi, iar semnul minus - în cadranele II și IV.

Într-adevăr, de exemplu, în primul trimestru și abscisă x. ordonată și y sunt punctul A1 pozitiv, atunci câtul x / y. și particular y / x - prin urmare, în mod pozitiv tangente și cotangentă au semne +. Un al doilea trimestru abscisa x - negativ, iar ordonata y - pozitiv, și, prin urmare, x / y. și y / x - negativă, în cazul în care tangenta și cotangentă au semnul minus.

Du-te la următoarea proprietatea sinus, cosinus, tangentă și cotangentă.

proprietate periodicitate

Acum ne vom ocupa, probabil, caracteristica cea mai evidentă a sinus, cosinus, tangenta și cotangentă unghiului. Este acest lucru: atunci când schimbați unghiul unui număr întreg de rotații complete ale sinus, cosinus, tangenta și cotangentă unghiului nu se schimba.

Acest lucru este de înțeles, atunci când unghiul de un număr întreg de rotații din punctul de plecare vom A va cădea întotdeauna la un punct A1 pe cercul unitate, prin urmare, valorile sinus, cosinus, tangentă și cotangentă rămân neschimbate, deoarece neschimbătoare coordonate punctul A1.

Cu ajutorul sinusului considerat proprietate, cosinus, tangenta, cotangentă, și poate fi scrisă ca: sin (α + 2 · π · z) = sinα. cos (α + 2 · π · z) = cosα. tg (α + 2 · π · z) = tgα. ctg (α + 2 · π · z) = ctgα. unde α - unghiul de rotație în radiani, z - orice număr întreg. Valoarea absolută care indică numărul de rotații complete care variază unghiul a. și semnul rotației indică direcția z.

Dacă unghiul a este dat în grade, formula menționată mai sus poate fi rescrisă ca sin (a + 360 ° · z) = sinα. cos (α + 360 ° · z) = cosα. tg (α + 360 ° · z) = tgα. ctg (α + 360 ° · z) = ctgα.

Exemple de utilizarea acestei proprietăți. De exemplu, deoarece, de asemenea. Iată un alt exemplu: sau.

Sinus considerate proprietate, cosinus, tangentă și cotangentă uneori numită proprietate periodicitate.

Proprietățile sinus, cosinus, tangentă și cotangentă opuse colțuri

Să A1 - punctul obținut ca urmare a activării punctului de start A (1, 0), în jurul unui punct O cu un unghi α. și punctul A2 - este rezultatul punctului A pivot la un unghi -α. colțul opus al α.

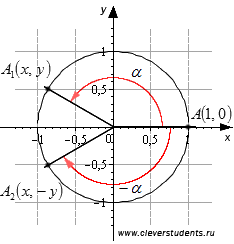
Proprietatea sinus, cosinus, tangentă și unghiurile opuse cotangentă bazate pe simplul fapt suficient: punctele mentionate mai sus A1 și A2 coincid, sau (dacă) sau sunt dispuse simetric în raport cu axa Ox. Adică, dacă punctul A1 are coordonatele (x, y). punctul A2 va avea coordonatele (x, -Y). Prin urmare, prin definițiile sinus, cosinus, tangentă și cotangentă egalitate înregistrare și.
Compararea lor ajung la raporturile dintre sinus, cosinus, tangentă și cotangentă unghiurile opuse a și speciile -a.
Aceasta este considerată o proprietate în formă de formule.

Exemple de utilizarea acestei proprietăți. De exemplu, egalitati și.

Rămâne doar să se constate că sinusurile proprietate, cosinusul, tangenta și cotangentă opuse colțuri ca proprietatea anterioară este adesea utilizată în calcularea valorii sinus, cosinus, tangentă și cotangentă, și vă permite să obțineți complet departe de unghiurile negative.